Diketahui:

Fungsi $g\left(x\right)=\sin 2x+5$ dengan $0\le x\le2\pi$

Ditanya:

Nilai balik maksimum dari fungsi $g(x)$ ?

Jawab:

Secara umum nilai stasioner adalah nilai $f\left(x\right)$ ketika $f'\left(x\right)=0$. Dengan demikian untuk mencari nilai stasioner terlebih dahulu dicari pembuat nol untuk $f'\left(x\right)$.

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sin (ax\pm b)$ turunannya adalah $y'=a\cos (ax\pm b)$

Untuk fungsi $y=a$ dengan $a$ suatu konstanta turunannya adalah $y'=0$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Pada soal diketahui fungsi $g\left(x\right)=\sin2x+5$. Diperoleh

$g'\left(x\right)=2\cos2x$

dengan pembuat nol

$g'\left(x\right)=0$

$\Leftrightarrow2\cos2x=0$

$\Leftrightarrow\cos2x=0$

$\Leftrightarrow\cos2x=\cos\frac{1}{2}\pi$

sebab $\cos\frac{1}{2}\pi=0$

Perlu diingat bahwa penyelesaian persamaan $\cos\left(ax+b\right)=\cos\theta$ adalah $ax+b=\theta+2k\pi$ atau $ax+b=-\theta+2k\pi$ sehingga untuk $\cos2x=\cos\frac{1}{2}\pi$ didapat

$2x=\frac{1}{2}\pi+2k\pi$

$\Leftrightarrow x=\frac{1}{4}\pi+k\pi$

untuk $k=0$ diperoleh $x=\frac{1}{4}\pi+0.\pi=\frac{1}{4}\pi$ memenuhi $0\le x\le2\pi$

untuk $k=1$ diperoleh $x=\frac{1}{4}\pi+1.\pi=\frac{5}{4}\pi$ memenuhi $0\le x\le2\pi$

atau

$2x=-\frac{1}{2}\pi+2k\pi$

$\Leftrightarrow x=-\frac{1}{4}\pi+k\pi$

untuk $k=0$ diperoleh $x=-\frac{1}{4}\pi+0.\pi=-\frac{1}{4}\pi$ tidak memenuhi $0\le x\le2\pi$

untuk $k=1$ diperoleh $x=-\frac{1}{4}\pi+1.\pi=\frac{3}{4}\pi$ memenuhi $0\le x\le2\pi$

untuk $k=2$ diperoleh $x=-\frac{1}{4}\pi+2.\pi=\frac{7}{4}\pi$ memenuhi $0\le x\le2\pi$

Artinya semua $x$ yang memenuhi adalah $x=\left\{\frac{1}{4}\pi,\ \frac{5}{4}\pi,\ \frac{3}{4}\pi,\ \frac{7}{4}\pi\right\}$

Secara umum ada tiga kondisi untuk nilai stasioner fungsi $f\left(x\right)$ untuk $x=c$. Hal ini dapat diperhatikan dari tanda $f'\left(x\right)$ disekitar $x=c$.

1. $f\left(x\right)$ mempunyai nilai balik maksimum $f\left(c\right)$ jika $f'\left(x\right)$ berganti tanda dari positif menjadi negatif saat melalui nol.
2. $f\left(x\right)$ mempunyai nilai balik minimum $f\left(c\right)$ jika $f'\left(x\right)$ berganti tanda dari negatif menjadi positif saat melalui nol.
3. $f\left(x\right)$ mempunyai titik belok horizontal pada $c$ jika $f'\left(x\right)$ tidak berganti tanda saat melalui nol.

Selanjutnya akan diperhatikan tanda $g'\left(x\right)$ disekitar $x=\left\{\frac{1}{4}\pi,\ \frac{5}{4}\pi,\ \frac{3}{4}\pi,\ \frac{7}{4}\pi\right\}$.

Untuk subinterval $\frac{1}{4}\pi\le x<\frac{3}{4}\pi$ dipilih $x=\frac{1}{2}\pi$ didapat

$g'\left(\frac{1}{2}\pi\right)=2\cos(2\cdot\frac{1}{2}\pi)=2\cos\pi=2(-1)=-2$ (negatif).

Untuk subinterval yang lain dicari dengan cara yang sama, sehingga diperoleh

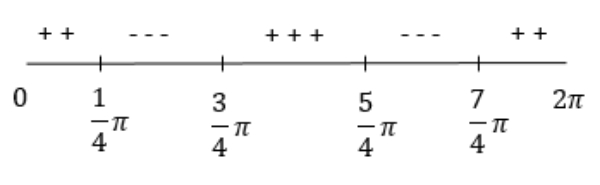
Yang diminta pada soal adalah nilai balik maksimum, yaitu $g'\left(x\right)$ berganti tanda dari positif menjadi negatif saat melalui nol. Hal tersebut terjadi pada $x=\frac{1}{4}\pi$ dan $x=\frac{5}{4}\pi$. Nilai balik maksimum tersebut adalah

$g\left(\frac{1}{4}\pi\right)=\sin2.\frac{1}{4}\pi+5$

$\Leftrightarrow g\left(\frac{1}{4}\pi\right)=\sin\frac{1}{2}\pi+5$

$\Leftrightarrow g\left(\frac{1}{4}\pi\right)=1+5$

$\Leftrightarrow g\left(\frac{1}{4}\pi\right)=6$

dan

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=\sin2.\frac{5}{4}\pi+5$

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=\sin\frac{5}{2}\pi+5$

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=\sin\left(2\pi+\frac{1}{2}\pi\right)+5$ karena $\sin\left(2\pi+\theta\right)=\sin\theta$ maka

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=\sin\frac{1}{2}\pi+5$

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=1+5$

$\Leftrightarrow g\left(\frac{5}{4}\pi\right)=6$