Diketahui:
cosecθ=−1517 dengan 23π<θ<2π
Ditanya:
Nilai dari tanθ=?
Dijawab:
Perlu diingat identitas pada trigonometri berikut:
tanθ=cotanθ1
⇔cotanθ=tanθ1
cotan2θ+1=cosec2θ
⇔cotan2θ=cosec2θ−1
Berdasarkan identitas trigonometri di atas diperoleh:
cotan2θ=cosec2θ−1
⇔cotan2θ=(−1517)2−1
⇔cotan2θ=225289−1
⇔cotan2θ=225289−225225
⇔cotan2θ=22564
⇔cotanθ=±158
⇔tanθ1=±158
⇔tanθ=±815
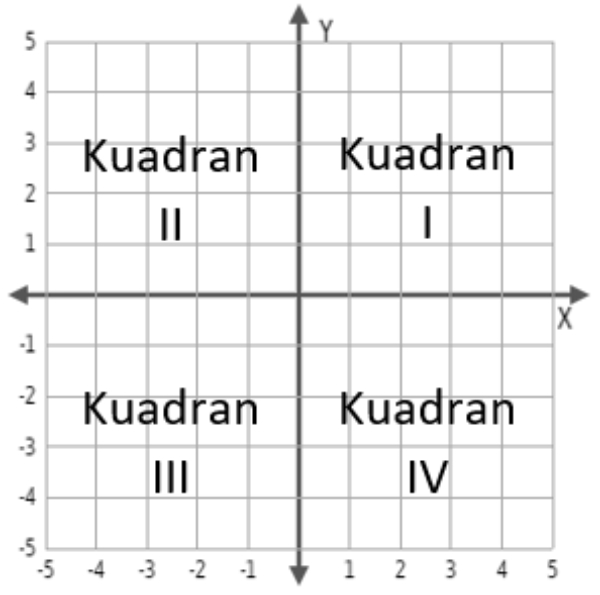
Perlu diingat bahwa sistem koordinat kartesius dibagi menjadi empat kuadran, yaitu
Kuadran I: sudut θ dengan 0°<θ<90°
Kuadran II: sudut θ dengan 90°<θ<180°
Kuadran III: sudut θ dengan 180°<θ<270°
Kuadran IV: sudut θ dengan 270°<θ<360°
atau jika diilustrasikan dalam sistem koordinat kartesius sebagai berikut:
Kita ubah terlebih dahulu batas nilai θ ke dalam ukuran derajat.
Pengubahan ukuran radian ke dalam ukuran derajat adalah:
θ⋅π180°
Untuk 23π diperoleh:
θ⋅π180°
=23π⋅π180°
=270°
Untuk 2π diperoleh:
θ⋅π180°
=2π⋅π180°
=360°
Karena 270°<θ<360°, maka sudut θ berada di kuadran IV.
Nilai trigonometri (sin, cos, tan) yang bernilai positif pada keempat kuadran tersebut disajikan pada gambar berikut:

Pada kuadran IV, nilai tanθ bernilai negatif, sehingga didapatkan:
tanθ=−815
Jadi, nilai dari tanθ adalah −815.