Perlu diingat bahwa sistem koordinat kartesius dibagi menjadi empat kuadran, yaitu
Kuadran I: sudut θ dengan 0°<θ<90° atau 0<θ<21π
Kuadran II: sudut θ dengan 90°<θ<180° atau 21π<θ<π
Kuadran III: sudut θ dengan 180°<θ<270° atau π<θ<23π
Kuadran IV: sudut θ dengan 270°<θ<360° atau 23π<θ<2π
dengan π=3,14
Artinya batas-batas kuadran tersebut adalah
0 radian,
21π=213,14=1,57 radian,
π=3,14 radian,
23π=233,14=4,71 radian, dan
2π=2.3,14=6,28 radian.
Nilai trigonometri (sin, cos, atau tan) yang bernilai positif pada keempat kuadran tersebut disajikan pada gambar berikut
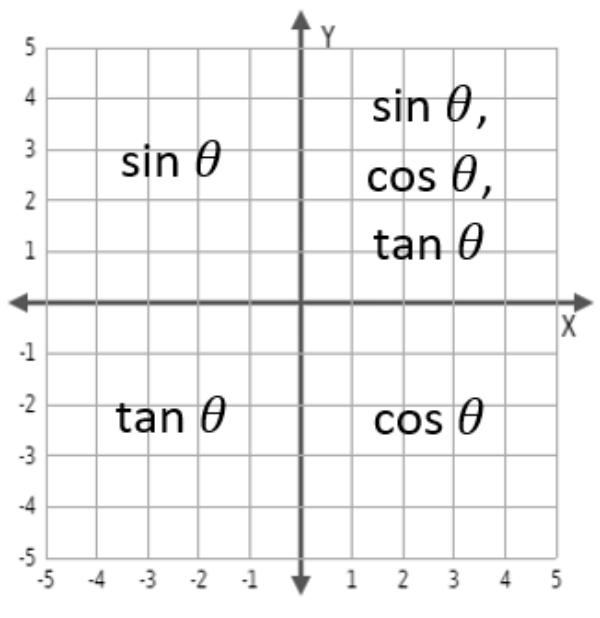
Karena 0<1<1,57 maka sudut 1 radian berada pada kuadran I. Didapat sin1 radian bernilai positif.
Karena 1,57<2<3,14 maka sudut 2 radian berada pada kuadran II. Didapat cos2 radian bernilai negatif.
Karena 1,57<3<3,14 maka sudut 3 radian berada pada kuadran II. Didapat sin3 radian bernilai positif.
Karena 3,14<4<4,71 maka sudut 4 radian berada pada kuadran III. Didapat tan4 radian bernilai positif.
Karena 4,71<5<6,28 maka sudut 5 radian berada pada kuadran IV. Didapat tan5 radian bernilai negatif.
Jadi pernyataan trigonometri tersebut yang mempunyai nilai positif adalah nomor 1, 3, dan 4