Diketahui:

$x^4-6x^3+mx^2+nx-8$

Dua akar pertama saling berlawanan: $x_1=-x_2\Leftrightarrow\ x_1+x_2=0$

Akar ketiga adalah dua kali akar keempat: $x_3=2x_4$

Ditanya:

$m=?$

$n=?$

Jawab:

Teorema akar-akar suku banyak.

Jika diketahui suatu suku banyak $ax^4+bx^3+cx^2+dx+e$, maka

$x_1+x_2+x_3+x_4=-\frac{b}{a}$

$x_1x_2+x_1x_3+x_1x_4+x_2x_3+x_2x_4+x_3x_4=\frac{c}{a}$

$x_1x_2x_3+x_1x_2x_4+x_1x_3x_4+x_2x_3x_4=-\frac{d}{a}$

$x_1x_2x_3x_4=\frac{e}{a}$

Diketahui suku banyak $x^4-6x^3+mx^2+nx-8$, maka

$a=1$

$b=-6$

$c=m$

$d=n$

$e=-8$

Diketahui $x_1+x_2=0$ dan $x_3=2x_4$, maka

$x_1+x_2+x_3+x_4=-\frac{b}{a}$

$\Leftrightarrow\ 0+2x_4+x_4=-\frac{\left(-6\right)}{1}$

$\Leftrightarrow\ 3x_4=6$

$\Leftrightarrow\ x_4=\frac{6}{3}$

$\Leftrightarrow\ x_4=2$

Sehingga diperoleh

$x_3=2x_4\ \Leftrightarrow\ x_3=4$

Kita dapat menentukan nilai $m$ dan $n$ dengan menggunakan akar-akar yang sudah diketahui.

Jika $f\left(x\right)=x^4-6x^3+mx^2+nx-8$ adalah suatu suku banyak dan $x_3=4$ adalah akar dari $f\left(x\right)$, maka $f\left(4\right)=0$ sehingga

$f\left(4\right)=0$

$\Leftrightarrow\ \left(4\right)^4-6\left(4\right)^3+m\left(4\right)^2+n\left(4\right)-8=0$

$\Leftrightarrow\ 256-6\left(64\right)+m\left(16\right)+4n-8=0$

$\Leftrightarrow\ 256-384+16m+4n-8=0$

$\Leftrightarrow\ -136+16m+4n=0$

$\Leftrightarrow\ 16m+4n=136$

$\Leftrightarrow\ 4m+n=34$ ...(1)

Jika $x_4=2$ adalah akar dari $f\left(x\right)$, maka $f\left(2\right)=0$ sehingga

$f\left(2\right)=0$

$\Leftrightarrow\ \left(2\right)^4-6\left(2\right)^3+m\left(2\right)^2+n\left(2\right)-8=0$

$\Leftrightarrow\ 16-6\left(8\right)+m\left(4\right)+2n-8=0$

$\Leftrightarrow\ 16-48+4m+2n-8=0$

$\Leftrightarrow\ -40+4m+2n=0$

$\Leftrightarrow\ 4m+2n=40$

$\Leftrightarrow\ 2m+n=20$ ...(2)

Eliminasikan persamaan (1) dan (2)

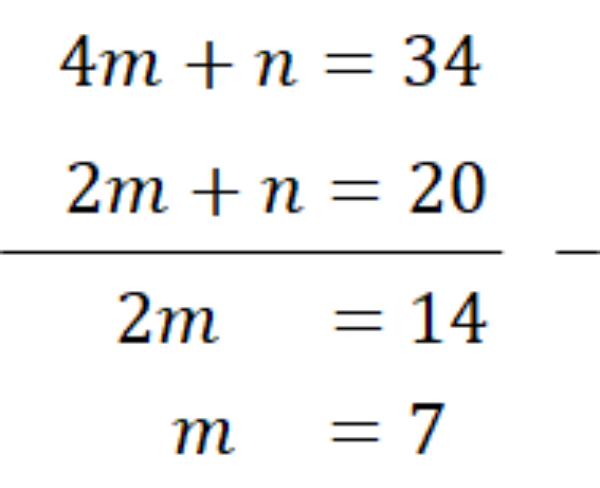
Substitusikan $m=7$ ke salah satu persamaan

$2m+n=20$

$\Leftrightarrow\ 2\left(7\right)+n=20$

$\Leftrightarrow\ 14+n=20$

$\Leftrightarrow\ n=20-14$

$\Leftrightarrow\ n=6$

Jadi, nilai $m$ dan $n$ berturut-turut adalah 7 dan 6.