Diketahui:
f:x→a+bsinx
f(2π)=1
f(6π)=2
Ditanya:
f(3π)=?
Jawab:
Langkah-langkah menyelesaikan persoalan di atas adalah sebagai berikut.
Membentuk sistem persamaan linear dua variabel
Karena f:x→a+bsinx dan f(2π)=1 maka diperoleh persamaan
f(2π)=1
a+bsin(2π)=1
a+b=1
Karena f:x→a+bsinx dan f(6π)=2 maka diperoleh persamaan
f(6π)=2
a+bsin(6π)=2
a+21b=2
Sehingga diperoleh sistem persamaan linear dua variabel
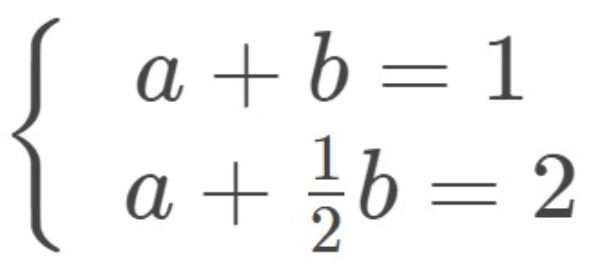
Menyelesaikan sistem persamaan dengan eliminasi-substitusi
Pertama lakukan eliminasi pada kedua persamaan
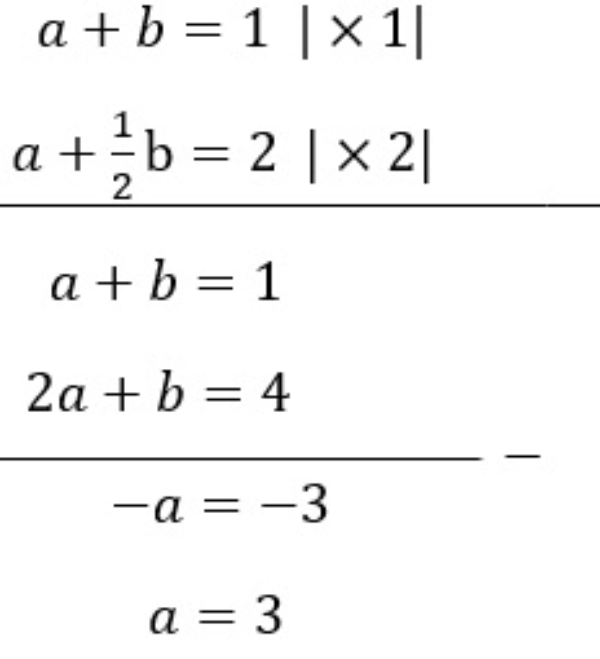
Selanjutnya substitusikan a=3 ke persamaan a+b=1
a+b=1
3+b=1
b=−2
Sehingga diperoleh f:x→3−2sinx
Maka
f(3π)=3−2sin(3π)
=3−2(213)
=3−3