Bank Soal Fisika SMA Keseimbangan Benda Tegar
Soal
Soal Populer Hari Ini
Ayah berangkat dari Bandung ke Bogor dan paman berangkat dari Bogor ke Bandung. Mereka akan melewati jalan yang sama. Ayah akan mengendarai mobil dengan kecepatan 40km/jam dan paman akan mengendarai sepeda motor dengan kecepatan 20km/jam . Jarak Bandung - Bogor 180 km. Mereka akan berangkat bersama-sama pada pukul 11.00. Mereka akan berpapasan pada pukul …
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Kecepatan
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Spelling
Berikut ini yang tidak termasuk ciri iklan baris yaitu ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Jenis-jenis Iklan
(1) Surat pengumuman
(2) Surat perizinan
(3) Undangan ulang tahun
(4) Undangan khitanan
Yang termasuk surat undangan tidak resmi adalah nomor ….
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Identifikasi Surat Undangan
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
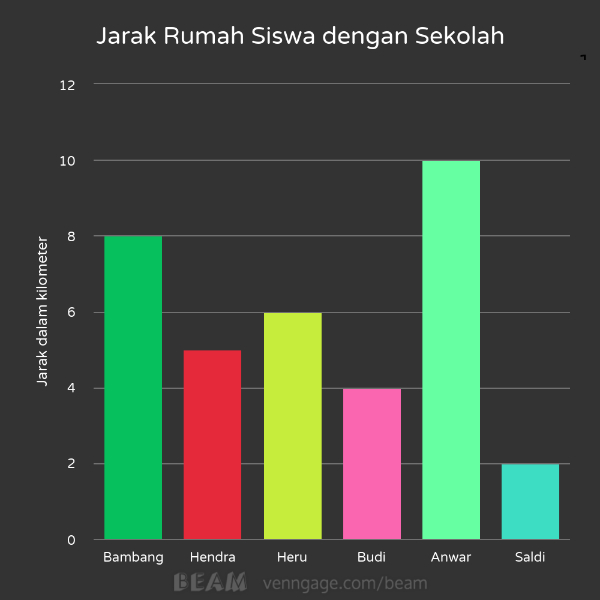
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Gambar di bawah ini yang bukan merupakan jaring-jaring kubus adalah …
Matematika
Level 5
Geometri
Balok dan Kubus
Sifat dan Jaring-Jaring Balok dan Kubus
Bagaimanakah cara menyamakan penyebut untuk operasi berikut?
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Look at the picture and complete the sentences.

Sometimes it is ... in autumn. I bring my ... everywhere.
Bahasa Inggris
Level 5
Bahasa Inggris
Weather and Season
Vocabulary: Weather Words
Hasil dari adalah ...
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Berbagai Bentuk Pecahan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Ayah berangkat dari Bandung ke Bogor dan paman berangkat dari Bogor ke Bandung. Mereka akan melewati jalan yang sama. Ayah akan mengendarai mobil dengan kecepatan 40km/jam dan paman akan mengendarai sepeda motor dengan kecepatan 20km/jam . Jarak Bandung - Bogor 180 km. Mereka akan berangkat bersama-sama pada pukul 11.00. Mereka akan berpapasan pada pukul …
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Berikut ini yang tidak termasuk ciri iklan baris yaitu ....
(1) Surat pengumuman
(2) Surat perizinan
(3) Undangan ulang tahun
(4) Undangan khitanan
Yang termasuk surat undangan tidak resmi adalah nomor ….
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Gambar di bawah ini yang bukan merupakan jaring-jaring kubus adalah …
Bagaimanakah cara menyamakan penyebut untuk operasi berikut?
Look at the picture and complete the sentences.
Sometimes it is ... in autumn. I bring my ... everywhere.
Hasil dari adalah ...







