Bank Soal Fisika SMA Pemantulan Cahaya
Soal
Soal Populer Hari Ini
Sebuah bak mandi memiliki panjang 150 cm, lebar 50 cm dan tinggi 80 cm. Jika bak tersebut dapat terisi penuh dalam waktu 10 menit, maka debit air yang mengalir dari keran adalah … liter/detik.
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Debit
Kelas V
Kurikulum 2013
K13
Matematika
Bagaimanakah cara menyamakan penyebut untuk operasi berikut?
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Kelas V
Kurikulum 2013
K13
Matematika
Pay attention to the pictures below.
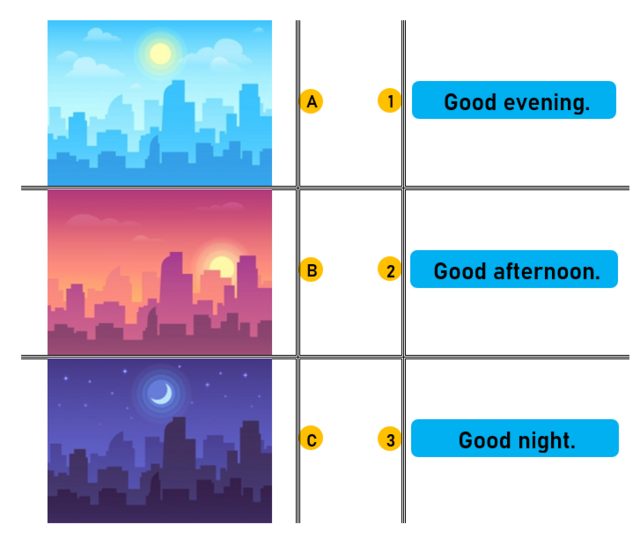
Match the pictures to the correct greetings and leave taking.
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Greeting & Leave Taking
Kelas V
Kurikulum 2013
K13
Cermati contoh surat berikut ini.

Paragraf penutup surat yang tepat adalah ...
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Menulis Surat Undangan

Andi mengikuti lomba menulis cerpen dalam iklan tersebut. Jika Andi berhasil menjadi juara II, hadiah yang berhasil didapatkan Andi adalah sertifikat dan uang sebesar ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Identifikasi Informasi
Seorang pebisnis telur ingin mengecek produksi telur. Diagram berikut menunjukkan hasil produksi telur dari bulan Januari hingga Juni.
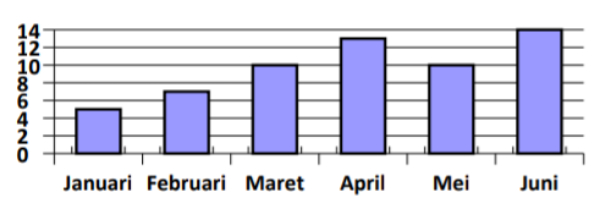
Produksi telur yang lebih dari 10 kuintal terjadi pada bulan ....
Matematika
Level 5,16
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
AKM
Asesmen Kompetensi Minimum
Personal
Data dan Ketidakpastian
Numerasi
Mengambil/Memperoleh
Level 3
Gambar di bawah ini yang bukan merupakan jaring-jaring kubus adalah …
Matematika
Level 5
Geometri
Balok dan Kubus
Sifat dan Jaring-Jaring Balok dan Kubus
Kelas V
Kurikulum 2013
K13
Matematika
Cermati teks berikut!
Siasat Bangau Tua

Alkisah hiduplah seekor bangau tua di pinggir sebuah telaga. Karena usianya sudah tua, ia tidak dapat lagi menangkap mangsanya di telaga sebanyak dulu lagi. Akibatnya, tubuhnya mengurus. Ia pun mencari akal untuk mendapatkan makanan supaya ia tidak mati kelaparan.
Pagi itu ia melaksanakan rencana yang sudah dipikirkannya semalaman. Ia duduk termenung di pinggir telaga dengan raut muka sedih. Ikan-ikan yang lewat di dekatnya pun tidak berusaha ditangkap seperti biasanya. Tindak tanduknya ini pun jadi pembicaraan hewan-hewan yang hidup di telaga. Akhirnya seekor katak penasaran dan menghampirinya,"Mengapa kamu terlihat sangat sedih dan tidak lagi memburu kami?" Jawab bangau,"Aku bersedih karena para manusia yang tinggal di sekitar telaga berencana untuk menimbun telaga dengan tanah. Kalau itu terjadi, semua makhluk dalam telaga akan mati. Aku pun akan mati kelaparan karenanya. Karena itu aku merasa sangat sedih."
Katak sangat terkejut mendengar hal ini dan segera memberitahukannya ke hewan-hewan lainnya di dalam telaga. Tak lama kemudian semua hewan di telaga telah mendengarnya dan merasa panik. Mereka mendatangi bangau untuk minta bantuan. Usul bangau,"Aku tahu ada telaga lain di dekat sini. Aku bisa mengantar kalian ke sana sebelum telaga ini ditimbun tanah. Tapi karena sudah tua, aku hanya bisa mengangkat satu hewan sekali jalan." Segera para hewan telaga menyetujuinya.
Sore itu ia mulai membawa hewan telaga satu per satu, dimulai dari ikan. Begitu sampai di tempat aman yang tak terlihat dari telaga, segera ia telan ikan itu. Lalu ia kembali lagi untuk mengambil ikan berikutnya hingga ia merasa kenyang. Hari demi hari tubuhnya semakin gemuk.
Suatu hari seekor kepiting meminta bangau untuk membawanya ke telaga sebelah. Bangau pun menyanggupinya. Ia terbang dengan membawa kepiting di paruhnya. Namun ketika akan hinggap di tempat biasanya, sang kepiting melihat tulang-tulang ikan yang berserakan. Ia langsung menyadari apa yang terjadi, dan mengancam bangau dengan melingkari lehernya dengan capitnya yang besar. Lalu ia usir sang bangau dan ia ceritakan jebakan bangau kepada hewan-hewan telaga. Para hewan telaga berterima kasih pada kepiting dan mengusungnya sebagai pahlawan.
Berdasarkan cerita dongeng di atas, yang terjadi setelah bangau menyampaikan berita tentang rencana manusia untuk menimbun telaga dengan tanah adalah ....
Bahasa Indonesia
Level 5,5
Membaca
Teks Fiksi dan Nonfiksi-Urutan Peristiwa
Menguraikan Urutan Peristiwa
Video
Perhatikan gambar jaring-jaring berikut!
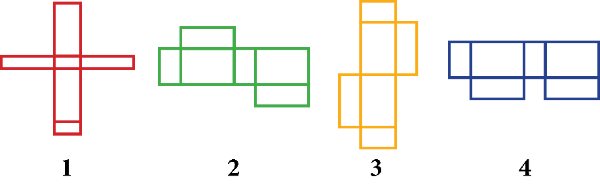
Gambar jaring-jaring balok yang benar ditunjukkan oleh nomor ....
Matematika
Level 5
Geometri
Balok dan Kubus
Sifat dan Jaring-Jaring Balok dan Kubus
Kelas V
Kurikulum 2013
K13
Matematika
Bacalah teks berikut dengan cermat!
Peristiwa pertempuran Ambarawa
Pada tanggal 20 Oktober 1945, pasukan sekutu dipimpin oleh Brigadir Jenderal Bethel mendarat di Semarang. Namun, kedatangannya diboncengi oleh tentara NICA (Netherland Indies Civil Administration). Tujuan kedatangannya untuk membebaskan para tawanan.
Saat sekutu dan NICA membebaskan tawanan tentara Belanda, para tawanan justru dipersenjatai. Ketegangan dimulai ketika tawanan Belanda bertindak sombong, serta mengabaikan kedaulatan pemerintah dengan terang-terangan berusaha untuk menduduki kembali Indonesia. Hal ini menimbulkan kemarahan rakyat Indonesia sehingga terjadilah pertempuran.
Pejuang Indonesia dipimpin oleh Letnan Kolonel M. Sarbini. Pada pertempuran tersebut, Letnal Kolonel Isdiman gugur sehingga Kolonel Sudirman turun langsung ikut bertempur. Siasat yang dipakai adalah mengadakan serangan serentak dari berbagai jurusan. Pada tanggal 12 Desember 1945 pasukan Indonesia melancarkan serangan serentak ke Ambarawa. Pada tanggal 15 Desember 1945 pasukan sekutu berhasil dibuat mundur kembali ke Semarang. Untuk mengenang pertempuran itu, setiap tanggal 15 Desember diperingati sebagai hari Infanteri dan didirikan monumen Palagan Ambarawa.
Makna kata gugur dalam paragraf ketiga pada teks tersebut adalah ....
Bahasa Indonesia
Level 5
Membaca
Teks Narasi Sejarah
Menggali Informasi
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sebuah bak mandi memiliki panjang 150 cm, lebar 50 cm dan tinggi 80 cm. Jika bak tersebut dapat terisi penuh dalam waktu 10 menit, maka debit air yang mengalir dari keran adalah … liter/detik.
Bagaimanakah cara menyamakan penyebut untuk operasi berikut?
Pay attention to the pictures below.
Match the pictures to the correct greetings and leave taking.
Cermati contoh surat berikut ini.
Paragraf penutup surat yang tepat adalah ...
Andi mengikuti lomba menulis cerpen dalam iklan tersebut. Jika Andi berhasil menjadi juara II, hadiah yang berhasil didapatkan Andi adalah sertifikat dan uang sebesar ....
Seorang pebisnis telur ingin mengecek produksi telur. Diagram berikut menunjukkan hasil produksi telur dari bulan Januari hingga Juni.
Produksi telur yang lebih dari 10 kuintal terjadi pada bulan ....
Gambar di bawah ini yang bukan merupakan jaring-jaring kubus adalah …
Cermati teks berikut!
Siasat Bangau Tua
Alkisah hiduplah seekor bangau tua di pinggir sebuah telaga. Karena usianya sudah tua, ia tidak dapat lagi menangkap mangsanya di telaga sebanyak dulu lagi. Akibatnya, tubuhnya mengurus. Ia pun mencari akal untuk mendapatkan makanan supaya ia tidak mati kelaparan.
Pagi itu ia melaksanakan rencana yang sudah dipikirkannya semalaman. Ia duduk termenung di pinggir telaga dengan raut muka sedih. Ikan-ikan yang lewat di dekatnya pun tidak berusaha ditangkap seperti biasanya. Tindak tanduknya ini pun jadi pembicaraan hewan-hewan yang hidup di telaga. Akhirnya seekor katak penasaran dan menghampirinya,"Mengapa kamu terlihat sangat sedih dan tidak lagi memburu kami?" Jawab bangau,"Aku bersedih karena para manusia yang tinggal di sekitar telaga berencana untuk menimbun telaga dengan tanah. Kalau itu terjadi, semua makhluk dalam telaga akan mati. Aku pun akan mati kelaparan karenanya. Karena itu aku merasa sangat sedih."
Katak sangat terkejut mendengar hal ini dan segera memberitahukannya ke hewan-hewan lainnya di dalam telaga. Tak lama kemudian semua hewan di telaga telah mendengarnya dan merasa panik. Mereka mendatangi bangau untuk minta bantuan. Usul bangau,"Aku tahu ada telaga lain di dekat sini. Aku bisa mengantar kalian ke sana sebelum telaga ini ditimbun tanah. Tapi karena sudah tua, aku hanya bisa mengangkat satu hewan sekali jalan." Segera para hewan telaga menyetujuinya.
Sore itu ia mulai membawa hewan telaga satu per satu, dimulai dari ikan. Begitu sampai di tempat aman yang tak terlihat dari telaga, segera ia telan ikan itu. Lalu ia kembali lagi untuk mengambil ikan berikutnya hingga ia merasa kenyang. Hari demi hari tubuhnya semakin gemuk.
Suatu hari seekor kepiting meminta bangau untuk membawanya ke telaga sebelah. Bangau pun menyanggupinya. Ia terbang dengan membawa kepiting di paruhnya. Namun ketika akan hinggap di tempat biasanya, sang kepiting melihat tulang-tulang ikan yang berserakan. Ia langsung menyadari apa yang terjadi, dan mengancam bangau dengan melingkari lehernya dengan capitnya yang besar. Lalu ia usir sang bangau dan ia ceritakan jebakan bangau kepada hewan-hewan telaga. Para hewan telaga berterima kasih pada kepiting dan mengusungnya sebagai pahlawan.
Berdasarkan cerita dongeng di atas, yang terjadi setelah bangau menyampaikan berita tentang rencana manusia untuk menimbun telaga dengan tanah adalah ....
Perhatikan gambar jaring-jaring berikut!
Gambar jaring-jaring balok yang benar ditunjukkan oleh nomor ....
Bacalah teks berikut dengan cermat!
Peristiwa pertempuran Ambarawa
Pada tanggal 20 Oktober 1945, pasukan sekutu dipimpin oleh Brigadir Jenderal Bethel mendarat di Semarang. Namun, kedatangannya diboncengi oleh tentara NICA (Netherland Indies Civil Administration). Tujuan kedatangannya untuk membebaskan para tawanan.
Saat sekutu dan NICA membebaskan tawanan tentara Belanda, para tawanan justru dipersenjatai. Ketegangan dimulai ketika tawanan Belanda bertindak sombong, serta mengabaikan kedaulatan pemerintah dengan terang-terangan berusaha untuk menduduki kembali Indonesia. Hal ini menimbulkan kemarahan rakyat Indonesia sehingga terjadilah pertempuran.
Pejuang Indonesia dipimpin oleh Letnan Kolonel M. Sarbini. Pada pertempuran tersebut, Letnal Kolonel Isdiman gugur sehingga Kolonel Sudirman turun langsung ikut bertempur. Siasat yang dipakai adalah mengadakan serangan serentak dari berbagai jurusan. Pada tanggal 12 Desember 1945 pasukan Indonesia melancarkan serangan serentak ke Ambarawa. Pada tanggal 15 Desember 1945 pasukan sekutu berhasil dibuat mundur kembali ke Semarang. Untuk mengenang pertempuran itu, setiap tanggal 15 Desember diperingati sebagai hari Infanteri dan didirikan monumen Palagan Ambarawa.
Makna kata gugur dalam paragraf ketiga pada teks tersebut adalah ....







