Diketahui:

Segitiga $ABC$ dengan $A\left(1,2\right),\ B\left(-1,-1\right),\ C\left(-4,4\right)$

Segitiga didilatasi dengan titik pusat $O\left(0,0\right)$ dan faktor skala 2

Ditanya:

Luas segitiga $ABC$$=?$

Jawab:

Secara umum bayangan titik $\left(x,y\right)$ yang didilatasi pada pusat $O\left(0,0\right)$ dengan faktor skala $k$ adalah $\left(x',y'\right)$ dengan

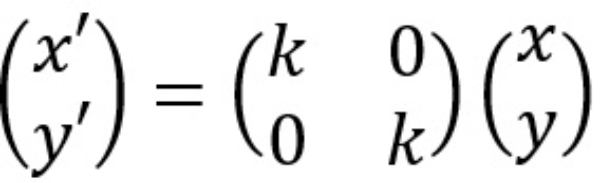
Diketahui segitiga $ABC$ dengan $A\left(1,2\right),\ B\left(-1,-1\right),\ C\left(-4,4\right)$ didilatasi dengan titik pusat $O\left(0,0\right)$ dan faktor skala 2.

Untuk $A\left(1,2\right)$

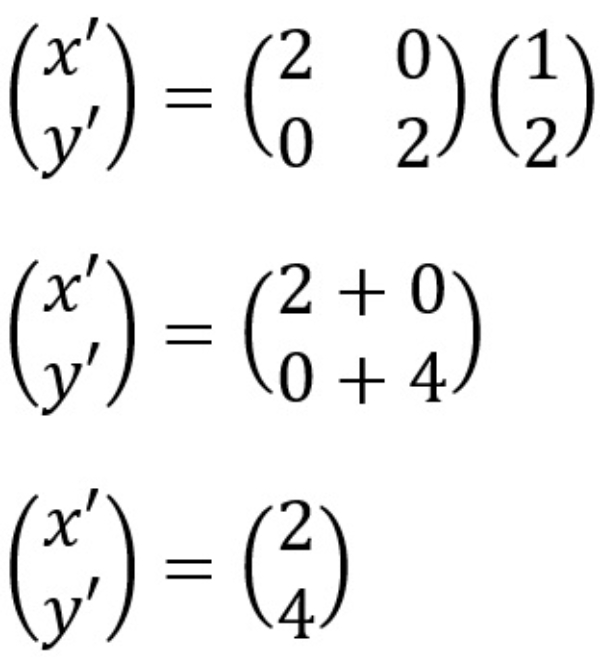
Sehingga didapatkan $A'\left(2,4\right)$

Untuk $B\left(-1,-1\right)$

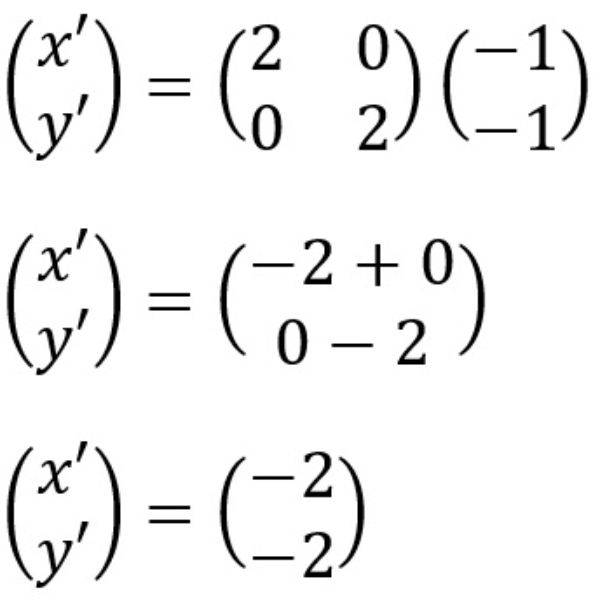
Sehingga didapatkan $B'\left(-2,-2\right)$

Untuk $C\left(-4,4\right)$

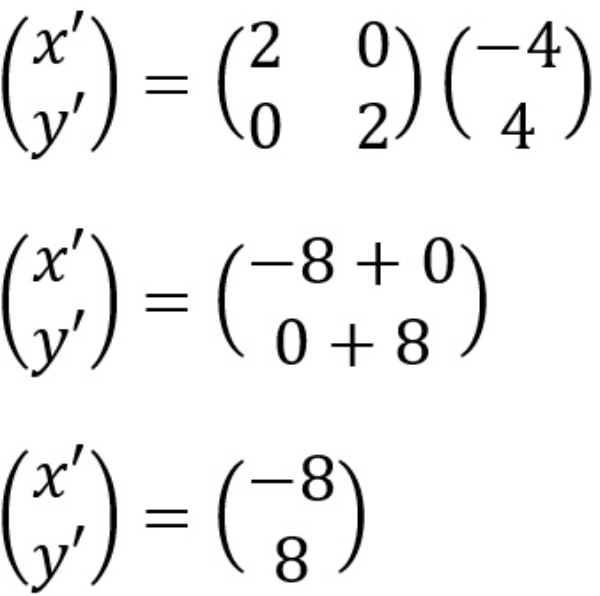
Sehingga didapatkan $C'\left(-8,8\right)$

Koordinat segitiga setelah didilatasi adalah $A'\left(2,4\right),\ B'\left(-2,-2\right),C'\left(-8,8\right)$ seperti yang digambarkan di bawah ini.

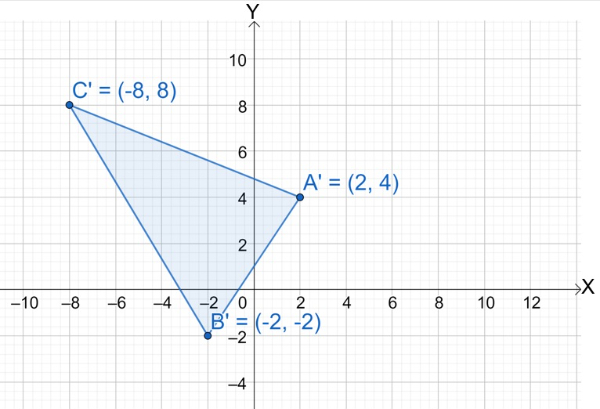
Luas segitiga $ABC$ dengan $A\left(a_1,b_1\right),B\left(a_2,b_2\right),C\left(a_3,b_3\right)$ adalah

$L=\frac{1}{2}\left|\left(a_1b_2+a_2b_3+a_3b_1\right)-\left(a_2b_1+a_3b_2+a_1b_3\right)\right|$

Dengan demikian, Luas segitiga $A'B'C'$ dengan $A'\left(2,4\right),\ B'\left(-2,-2\right),C'\left(-8,8\right)$ adalah

$L=\frac{1}{2}\left|\left(\left(2\right)\left(-2\right)+\left(-2\right)\left(8\right)+\left(-8\right)\left(4\right)\right)-\left(\left(-2\right)\left(4\right)+\left(-8\right)\left(-2\right)+\left(2\right)\left(8\right)\right)\right|$

$L=\frac{1}{2}\left|\left(-4-16-32\right)-\left(-8+16+16\right)\right|$

$L=\frac{1}{2}\left|-52-24\right|$

$L=\frac{1}{2}\left|-76\right|$

$L=38$ satuan

Jadi, luas segitiga setelah didilatasi adalah 38 satuan.