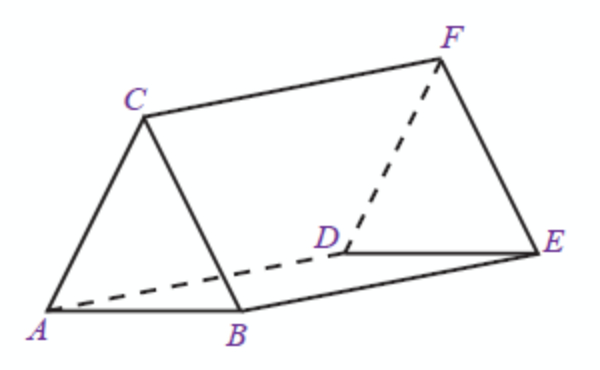
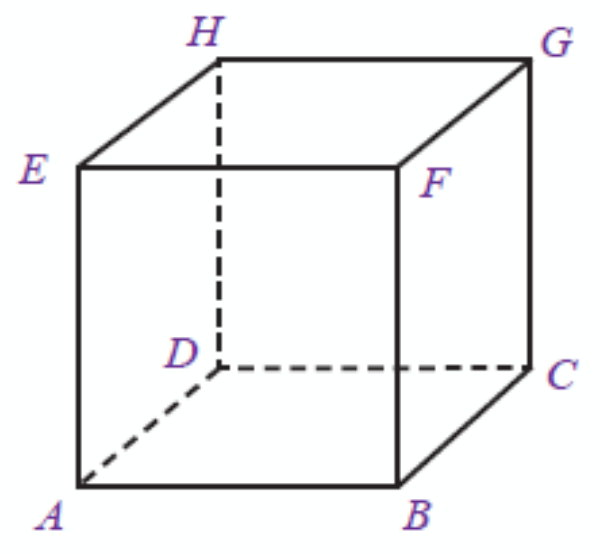
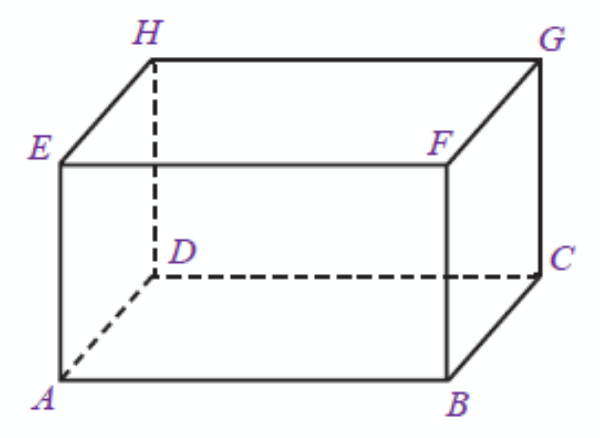
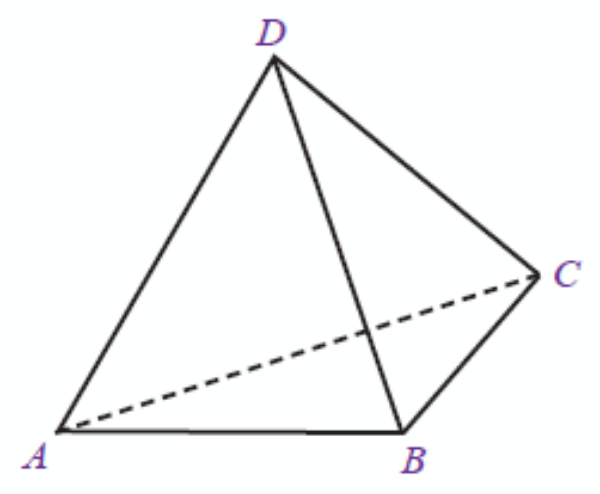
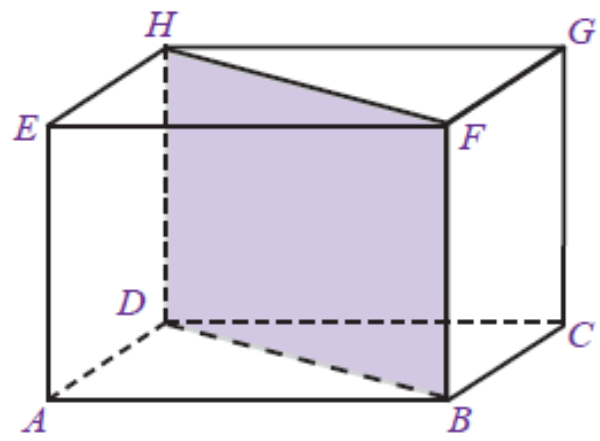
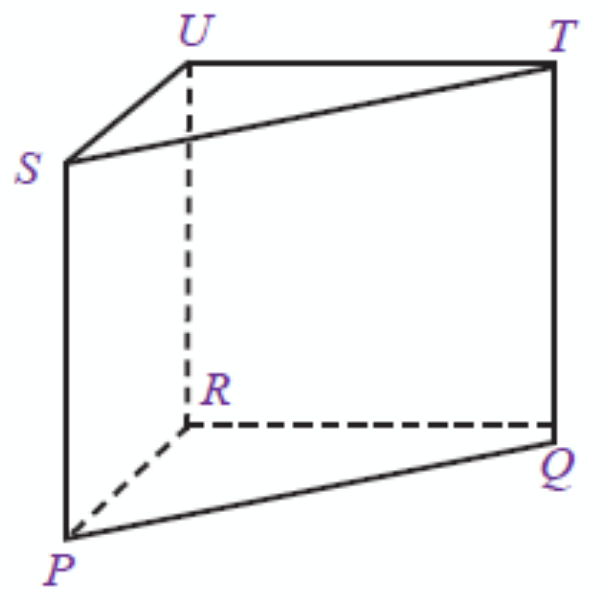
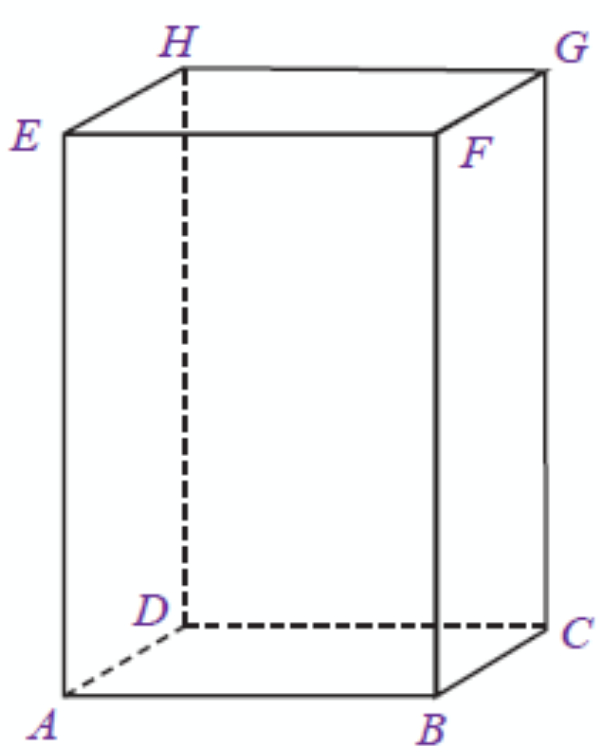
Latihan Matematika Kelas VIII Unsur dan Ciri Bangun Ruang Sisi Datar

Admin Cube
Soal
10
Kesulitan
Reguler
Waktu
∞
Mata Pelajaran
Matematika
Selesai
∞
Benar
0
Salah
0
Dilewati
10
Komposisi Skor
Peringkat
| 1. | 5 |
|---|---|
| 2. | 3 |
| 3. | 2 |
| 4. | 0 |
| 5. | 0 |
| 6+. | 0 |
Tidak Ada Komentar
Ayo Daftar Sekarang!
Dan dapatkan akses ke seluruh 151.115 soal dengan berbagai tingkat kesulitan!
DaftarMasih ada yang belum ngerti juga? Tanya ke kak tutor aja! Caranya, daftar layanan premium dan pilih paketnya.