Diketahui :

$PQ\ =\ 12\ \text{}$ cm

$QR\ =\ 16$ cm

$t=24$ cm

Ditanya :

Jarak titik $P$ dengan garis $TR$

Dijawab :

Jarak titik ke garis adalah panjang ruas garis dari titik yang tegak lurus dengan garis.

Perhatikan gambar berikut.

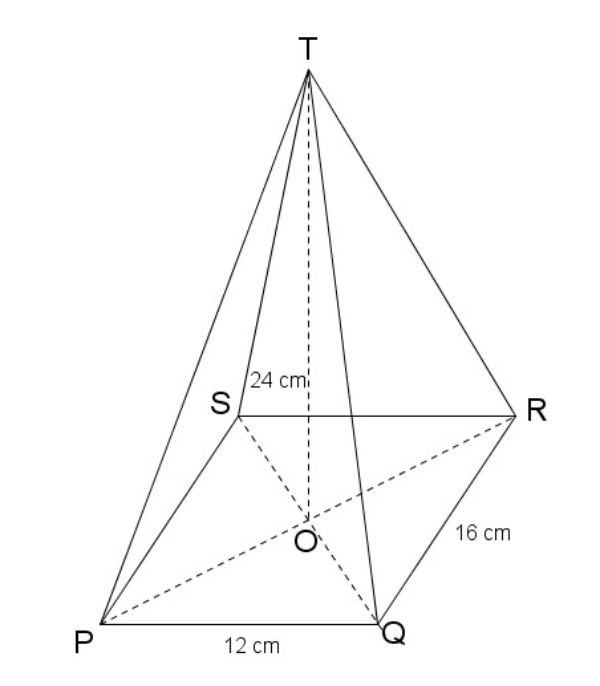
Pertama, dicari terlebih dahulu panjang $PR$ dengan mengaplikasikan teorema pythagoras.pada $\triangle PQR$

$PR=\sqrt{PQ^{2\ }+Q^2}\$

$=\sqrt{12^2+16^2}$

$=\sqrt{144+256}$

$=\sqrt{400}$

$=20$ cm

Karena $O$ titik tengah dari $PR$, maka $OR\ =\ \frac{PR}{2}=\ \frac{20}{2}=10$ cm.

Selanjutnya perhatikan $\triangle TOR$ siku-siku di $O$. Dengan menggunakan teorema pythagoras diperoleh

$TR\ =\ \sqrt{OR^{2\ }+OT^2}$

$=\sqrt{10^2+24^2}$

$=\sqrt{100+576}$

$=\sqrt{676}$

$=26$ cm

Perhatikan $\triangle PTR$ berikut.

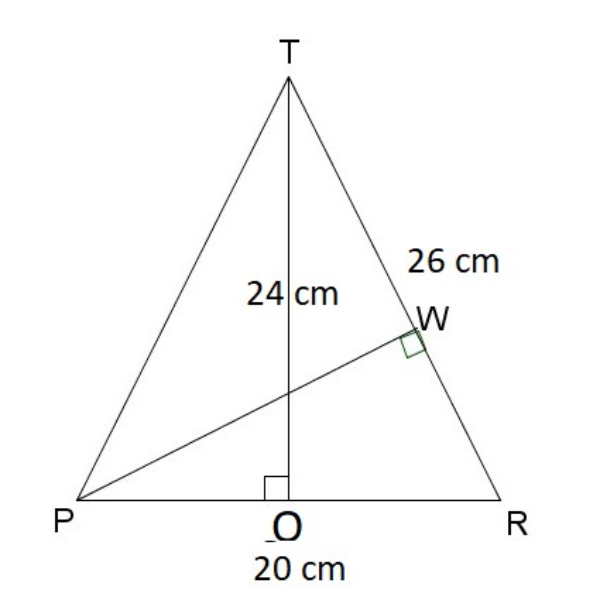
Jarak titik $P$ ke garis $TR$ sama dengan panjang ruas garis $PW$. Untuk mencari $$ $PW$ digunakan rumus dari luas segitiga berikut.

$\frac{1}{2}\times PR\ \times OT\ =\ \frac{1}{2}\times TR\ \times PW$

$20\ \times24\ =\ 26\times PW$

$PW\ =\ \frac{20\ \times24}{26}=\frac{480}{26}=18\ \frac{6}{13}$ cm

Jadi, jarak titik $P$ ke garis $TR$ adalah $18\ \frac{6}{13}$ cm.