1) Mencari titik potong sumbu- x dan sumbu-y tiap pertidaksamaan


2) Gambar grafik dan menentukan titik-titik pojok
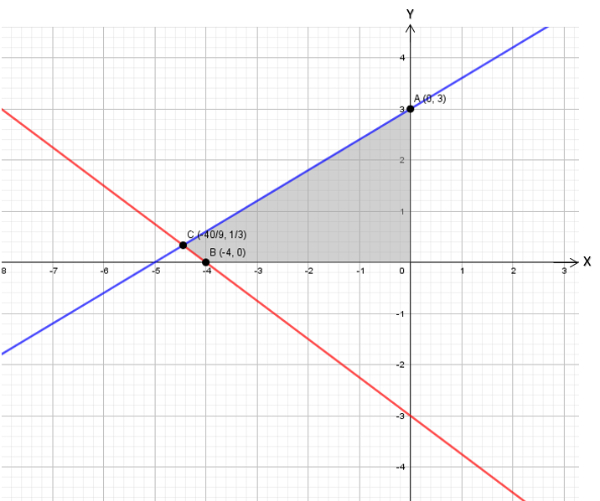
Koordinat di titik C
Mencari nilai y menggunakan metode eliminasi.
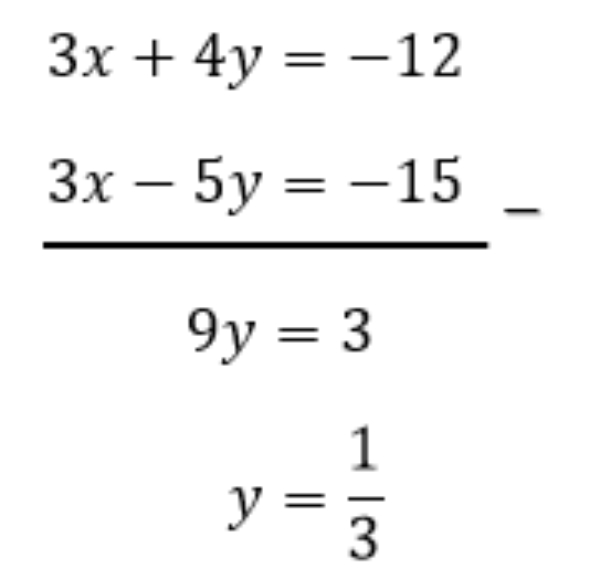
Menentukan nilai x menggunakan metode substitusi
3x+4y=−12, di mana y=31
3x+4(31)=−12
3x=−12−34
3x=3−36−4=−340
x=−940
Titik-titik pojoknya adalah:
A=(0, 3)
B=(−4, 0)
C=(−940, 31)
3) Nilai Optimum

Jadi, nilai maksimum dari f(x,y)=3x−2y adalah -6