Diketahui:

Pertidaksamaan $\frac{x-6}{x+1}\le\frac{x-4}{x+2}$.

Ditanya:

Penyelesaian pertidaksamaan tersebut?

Jawab:

Pertidaksamaan pada soal dapat diubah menjadi

$\frac{x-6}{x+1}\le\frac{x-4}{x+2}$

$\Leftrightarrow\frac{x-6}{x+1}-\frac{x-4}{x+2}\le0$

$\Leftrightarrow\frac{\left(x-6\right)\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}-\frac{\left(x-4\right)\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}\le0$

$\Leftrightarrow\frac{\left(x-6\right)\left(x+2\right)-\left(x-4\right)\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}\le0$

$\Leftrightarrow\frac{\left(x^2-4x-12\right)-\left(x^2-3x-4\right)}{x^2+3x+2}\le0$

$\Leftrightarrow\frac{x^2-4x-12-x^2+3x+4}{x^2+3x+2}\le0$

$\Leftrightarrow\frac{x^2-x^2-4x+3x-12+4}{x^2+3x+2}\le0$

$\Leftrightarrow\frac{-x-8}{x^2+3x+2}\le0$ . . . (*)

Pertidaksamaan (*) merupakan pertidaksamaan rasional linear-kuadrat. Perlu diingat pertidaksamaan rasional linear-kuadrat memiliki bentuk umum sebagai berikut:

$\frac{ax^2+bx+x}{px+q}\le n$ atau $\frac{px+q}{ax^2+bx+x}\le n$

dengan $a,\ b,\ c,\ p,\ q,$ dan $n$ merupakan konstanta. Tanda pertidaksamaan $\le$ dapat juga berbentuk $<,\ \ge,$ atau $>$

Cara menyelesaikan pertidaksamaan rasional linear-kuadrat adalah dengan

1. Mencari harga nol dari pertidaksamaan tersebut, dengan mengganti tanda pertidaksamaan menjadi tanda sama dengan (=), kemudian mencari nilai nol untuk pembilang maupun penyebut. Perlu diingat bahwa penyebut tidak boleh sama dengan nol.
2. Mencari nilai $x$ yang sesuai dengan tanda pertidaksamaannya.

Akan dicari harga nol dari pertidaksamaan (*). Diperoleh

$\frac{-x-8}{x^2+3x+2}=0$

Untuk pembilang diperoleh

$-x-8=0$

$\Leftrightarrow-8=x$

Untuk penyebut diperoleh

$x^2+3x+2=0$ . . . (**)

Nilai $p,\ q$ sehingga $p+q=3$ dan $pq=2$ adalah $p=1$ dan $q=2$

Akibatnya persamaan (**) dapat difaktorkan menjadi

$\left(x+p\right)\left(x+q\right)=0$

$\Leftrightarrow\left(x+1\right)\left(x+2\right)=0$

Artinya

$x+1=0\Leftrightarrow x=-1$ atau

$x+2=0\Leftrightarrow x=-2$

Karena $x=-1$ dan $x=-2$ diperoleh dari penyebut dan penyebut tidak boleh sama dengan nol, maka $x=-1$ dan $x=-2$ tidak memenuhi pertidaksamaan (*).

Berdasarkan harga nol yang diperoleh, pertidaksamaan (*) dapat ditulis menjadi

$\frac{-x-8}{\left(x+1\right)\left(x+2\right)}\le0$ 

$\Leftrightarrow\frac{-1\left(x+8\right)}{\left(x+1\right)\left(x+2\right)}\le0$ . . . (***)

Diperhatikan tabel yang menunjukkan tanda nilai yang diperoleh pada batasan/interval yang ada.

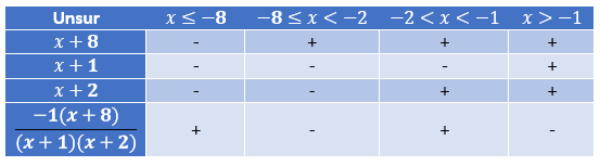
Jika dinyatakan dalam garis bilangan sebagai berikut

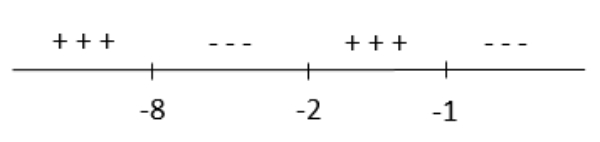
Pertidaksamaan (***) memiliki tanda $\le$ artinya yang diminta adalah hasil dengan tanda negatif dan $x=-8$merupakan penyelesaian (sebab memuat sama dengan). Diperoleh

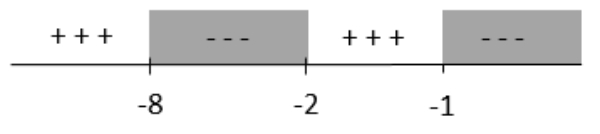
Jadi penyelesaian dari pertidaksamaan tersebut adalah $-8\le x<-2$ atau $x>-1$