Diketahui:

$\lim\limits_{x\to a}\left[f\left(x\right)-2g\left(x\right)\right]=4$

$\lim\limits_{x\to a}\left[2f\left(x\right)+g\left(x\right)\right]=3$

Ditanya:

$\lim\limits_{x\to a}\left[\frac{f\left(x\right)}{g\left(x\right)}\right]=?$

Jawab:

Jika $f$ dan $g$ fungsi-fungsi dari $x$ dan $c$ adalah suatu konstanta, maka

$\lim\limits_{x\to c}\left[f\left(x\right)\pm g\left(x\right)\right]=\lim\limits_{x\to c}f\left(x\right)\pm\lim\limits_{x\to c}g\left(x\right)$

$\lim\limits_{x\to a}\left[\frac{f\left(x\right)}{g\left(x\right)}\right]=\frac{\lim\limits_{x\to a}f\left(x\right)}{\lim\limits_{x\to a}g\left(x\right)}$

Dengan demikian,

$\lim\limits_{x\to a}\left[f\left(x\right)-2g\left(x\right)\right]=4$

$\lim\limits_{x\to a}f\left(x\right)-2\lim\limits_{x\to a}g\left(x\right)=4$

kemudian

$\lim\limits_{x\to a}\left[2f\left(x\right)+g\left(x\right)\right]=3$

$2\lim\limits_{x\to a}f\left(x\right)+\lim\limits_{x\to a}g\left(x\right)=3$

Misalkan $\lim\limits_{x\to a}f\left(x\right)=m$ dan $\lim\limits_{x\to a}g\left(x\right)=n$ maka terbentuk sistem persamaan linear

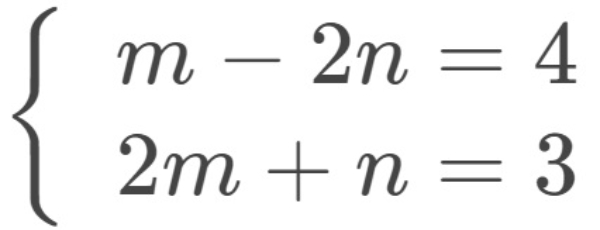
Selesaikan dengan eliminasi

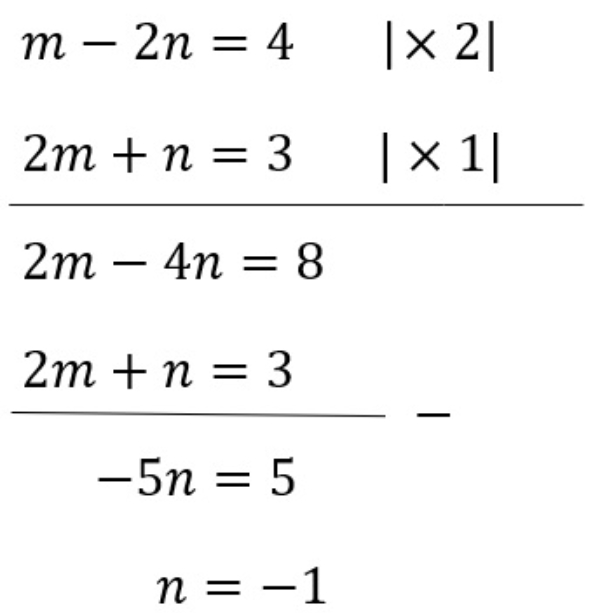
Substitusikan nilai $n=-1$ ke $m-2n=4$

$m-2n=4$

$m-2\left(-1\right)=4$

$m+2=4$

$m=2$

maka

$\lim\limits_{x\to a}\left[\frac{f\left(x\right)}{g\left(x\right)}\right]=\frac{\lim\limits_{x\to a}f\left(x\right)}{\lim\limits_{x\to a}g\left(x\right)}$

$=\frac{m}{n}$

$=\frac{2}{-1}$

$=-2$