Diketahui:

Massa balok 1 $m_1$ = 3 kg

Massa balok 2 $m_2$ = 3 kg

Sudut kemiringan $θ$ = $37°$

Koefisien gesek kinetik balok 1 dan lantai $\mu_{\text{k1}}$ = 0,2

Koefisien gesek kinetik balok 2 dan lantai $\mu_{\text{k2}}$ = 0,5

Ditanya:

Percepatan sistem $a$ = ?

Jawab:

Terdapat empat gaya yang bekerja pada sistem yaitu gaya berat, gaya tegangan tali, gaya normal dan gaya gesek. Gaya berat adalah gaya yang dipengaruhi oleh gravitasi bumi dan arahnya selalu menuju ke pusat bumi. Gaya tegangan tali adalah gaya pada ujung-ujung tali yang terjadi akibat kondisi tali yang tegang. Gaya normal adalah gaya tegak lurus permukaan bidang sentuh. Dan gaya gesek adalah gaya yang terjadi akibat adanya dua benda yang saling bergesekan.

Untuk menyelesaikan kasus ini, gunakan hukum II Newton $ΣF=Σma$ dengan meninjau masing-masing benda. Uraikan terlebih dahulu gaya-gaya yang bekerja pada sumbu-X dan sumbu-Y seperti pada gambar berikut. Anggap arah kanan sebagai sumbu-X positif, sebaliknya arah kiri sebagai sumbu-X negatif. Serta arah atas sebagai sumbu-Y positif dan arah bawah sebagai sumbu-Y negatif.

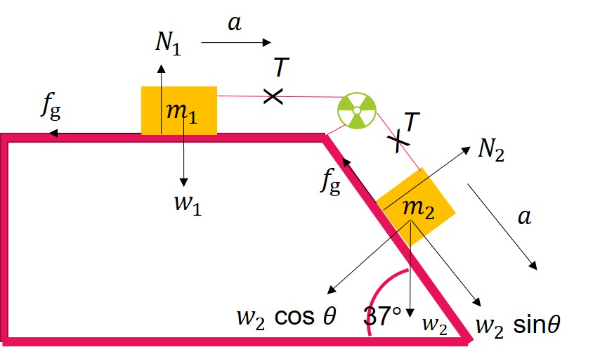
(1) Tinjau balok 1

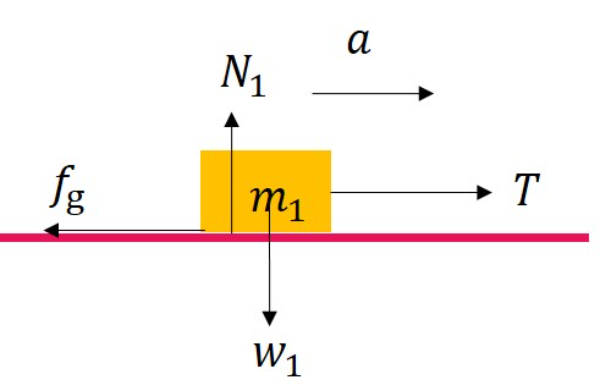
Karena balok 1 bergerak ke arah horizontal, maka $ΣF_y=0.$

$ΣF_y=0$

$N_1-w_1=0$

$N_1=w_1$

$=m_1g$ ... (1)

Substitusikan persamaan (1) ke dalam tinjauan sumbu-X pada balok 1.

$ΣF_x=Σma$

$T-f_{\text{g}}=m_1a$

$T-μ_{\text{k}}N_1=m_1a$

$T-μ_{\text{k}1}N_1=m_1a$

$T-μ_{\text{k}1}m_1g=m_1a$

$T=m_1a+μ_{\text{k}1}m_1g$

$=3a+\left(0,2\right)\left(3\right)\left(10\right)$

$=3a+6$ ... (2)

(2) Tinjau balok 2

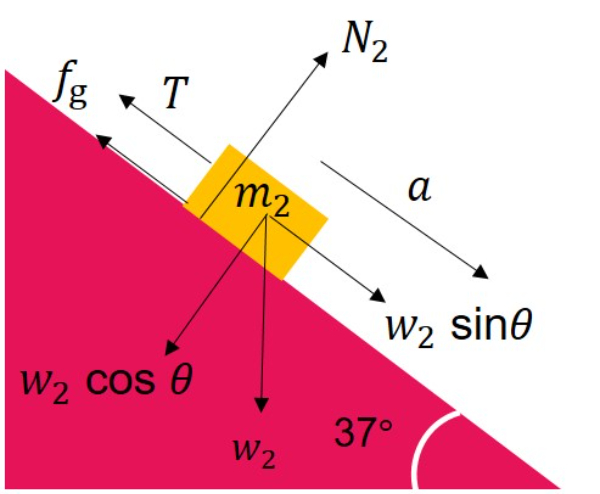
Karena balok 2 bergerak ke arah horizontal maka $ΣF_y=0.$

$ΣF_y=0$

$N_2-w_2\cosθ=0$

$N_2=w_2\cos37°$

$=m_2g\cos37°$

$=\left(3\right)\left(10\right)\left(0,8\right)$

$$ $=24$ N

Substitusikan nilai $N_2$ ke dalam tinjauan sumbu-X pada balok 2.

$ΣF_x=Σma$

$w_2\sinθ-T-f_{\text{g}}=m_2a$

$m_2g\sinθ-T-f_{\text{g}}=m_2a$

$T=m_2g\ \sinθ-f_{\text{g}}-m_2a$

$=\left(3\right)\left(10\right)\sinθ-μ_{\text{k}2}N_2-3a$

$=\left(30\right)\sin37°-\left(0,5\right)\left(24\right)-3a$

$=\left(30\right)\left(0,6\right)-\left(0,5\right)\left(24\right)-3a$

$=18-12-3a$

$=6-3a$ ... (3)

Substitusikan persamaan (2) dan (3).

$3a+6=6-3a$

$3a+3a=6-6$

$6a=0$

$a=0\$m/s²

Jadi, percepatan sistem adalah 0 m/s² yang berarti sistem dalam keadaan seimbang.