Secara umum bayangan titik $\left(x,y\right)$ yang didilatasi pada pusat $P\left(a,b\right)$ dengan faktor skala $k$ adalah $\left(x',y'\right)$ dengan

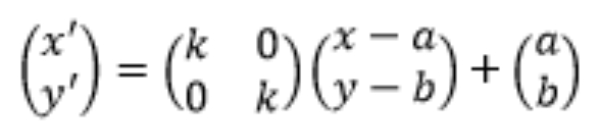
Dimisalkan $\left(x,y\right)$ merupakan titik pada lingkaran $(x-1)^2+(y-1)^2=16$ dan $\left(x',y'\right)$ merupakan bayangan titik $\left(x,y\right)$ yang didilatasi terhadap pusat $P\left(-1,-2\right)$ dengan faktor skala $-2$

Berdasarkan yang diketahui di soal diperoleh $k=-2$ sehingga

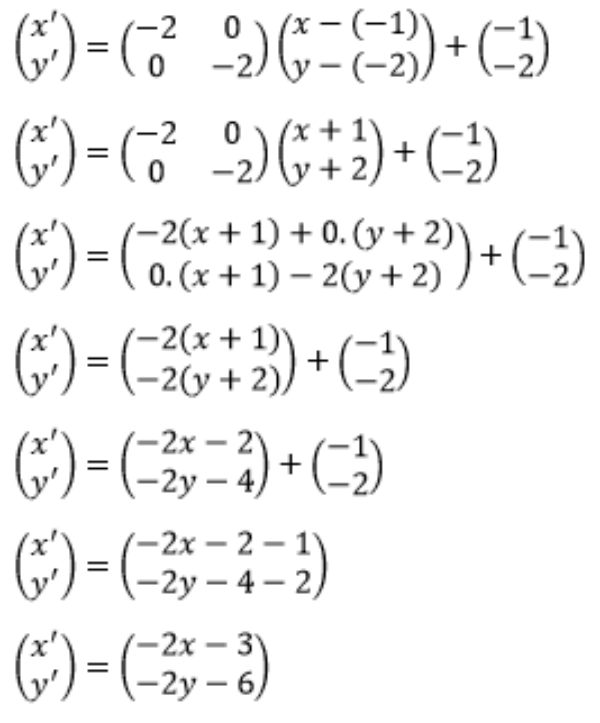
Artinya

$x'=-2x-3\ \Rightarrow\ 2x=-x'-3\ \Rightarrow\ x=\frac{-x'-3}{2}$ dan

$y'=-2y-6\ \Rightarrow\ 2y=-y'-6\ \Rightarrow\ y=\frac{-y'-6}{2}$

Substitusikan $x=\frac{-x'-3}{2}$ dan $y=\frac{-y'-6}{2}$ pada $(x-1)^2+(y-1)^2=16$ didapat

$(x-1)^2+(y-1)^2=16$

$(\frac{-x'-3}{2}-1)^2+(\frac{-y'-6}{2}-1)^2=16$

$(\frac{-x'-3-2}{2})^2+(\frac{-y'-6-2}{2})^2=16$

$(\frac{-x'-5}{2})^2+(\frac{-y'-8}{2})^2=16$

$\frac{(x'+5)^2}{4}+\frac{(y'+8)^2}{4}=16$

$4\left(\frac{(x'+5)^2}{4}+\frac{(y'+8)^2}{4}\right)=4.16$

$(x'+5)^2+(y'+8)^2=64$

Jadi persamaan bayangan lingkaran $(x-1)^2+(y-1)^2=16$ oleh dilatasi pada pusat $P\left(-1,-2\right)$ dengan faktor skala $-2$ adalah

$(x+5)^2+(y+8)^2=64$