Langkah-langkah penyelesaian sistem persamaan linear tiga variabel menggunakan metode eliminasi-substitusi adalah sebagai berikut.

Eliminasikan salah satu variabel dari dua persamaan

Pada persoalan di atas pilih persamaan (1) dan (2) untuk mengeliminasi variabel $y$ sehingga diperoleh

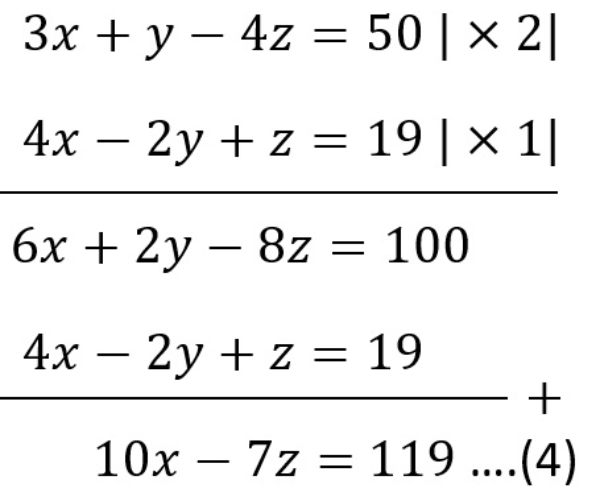
Pilih persamaan (2) dan (3) untuk mengeliminasi variabel $y$ sehingga diperoleh

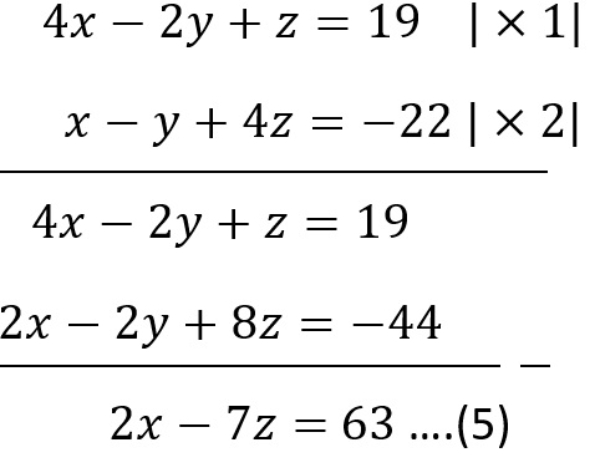
Selesaikan sistem persamaan linear dua variabel yang diperoleh

Diperoleh sistem persamaan linear dua variabel yaitu

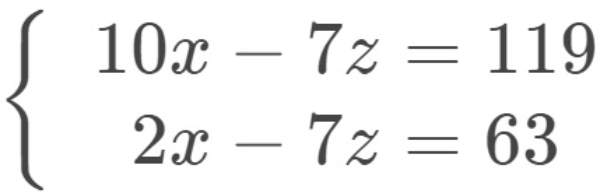
Selesaikan dengan metode eliminasi-substitusi

Proses eliminasi

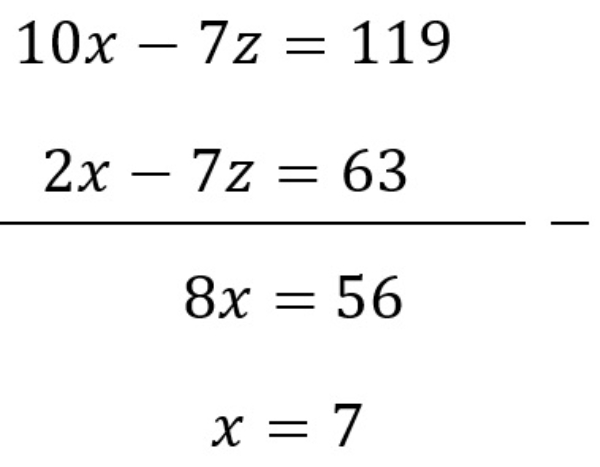
Proses substitusi

Substitusikan nilai $x=7$ ke persamaan (5)

$2x-7z=63$

$2\left(7\right)-7z=63$

$14-7z=63$

$-7z=49$

$z=-7$

Substitusikan nilai $x=7$ dan $z=-7$ ke persamaan (1)

$3x+y-4z=50$

$3\left(7\right)+y-4\left(-7\right)=50$

$21+y+28=50$

$y+49=50$

$y=1$

sehingga diperoleh penyelesaian $x=7,\ y=1,\ z=-7$

Periksa nilai penyelesaian

Pada persamaan (1)

$3x+y-4z=50$

$3\left(7\right)+1-4\left(-7\right)=50$

$21+1+28=50$

$50=50$ (benar)

Pada persamaan (2)

$4x-2y+z=19$

$4\left(7\right)-2\left(1\right)+\left(-7\right)=19$

$28-2-7=19$

$19=19$ (benar)

Pada persamaan (3)

$x-y+4z=-22$

$7-1+4\left(-7\right)=-22$

$7-1-28=-22$

$-22=-22$ (benar)

maka

$HP=\left\{\left(7,1,-7\right)\right\}$