Langkah-langkah penyelesaian sistem persamaan linear tiga variabel menggunakan metode eliminasi-substitusi adalah sebagai berikut.

Eliminasikan salah satu variabel dari dua persamaan

Pada persoalan di atas pilih persamaan (1) dan (3) sehingga diperoleh

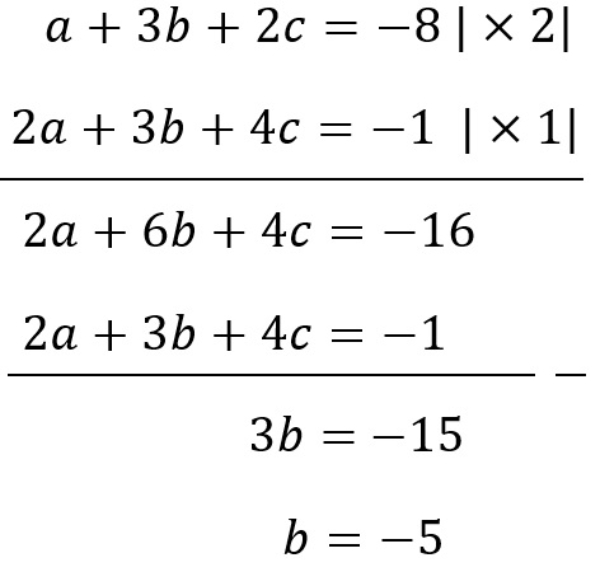
Pilih persamaan (1) dan (2) untuk mengeliminasi variabel $c$ sehingga diperoleh

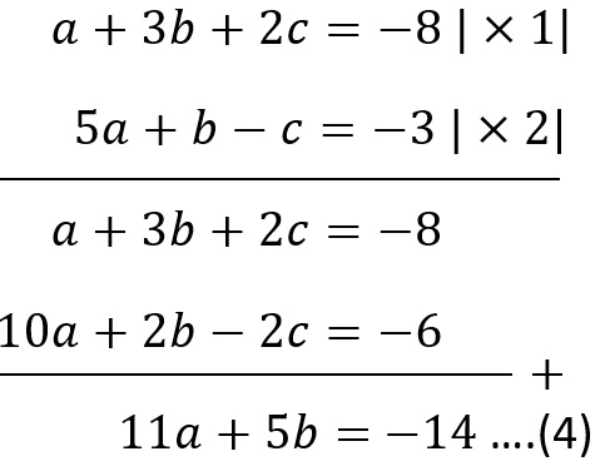
Proses substitusi

Substitusikan nilai $b=-5$ ke persamaan (4)

$11a+5b=-14$

$11a+5\left(-5\right)=-14$

$11a-25=-14$

$11a=11$

$a=1$

Substitusikan nilai $a=1$ dan $b=-5$ ke persamaan (1)

$a+3b+2c=-8$

$1+3\left(-5\right)+2c=-8$

$1-15+2c=-8$

$-14+2c=-8$

$2c=6$

$c=3$

sehingga diperoleh penyelesaian $a=1,\ b=-5,\ c=3$

Periksa nilai penyelesaian

Pada persamaan (1)

$a+3b+2c=-8$

$1+3\left(-5\right)+2\left(3\right)=-8$

$1-15+6=-8$

$-8=-8$ (benar)

Pada persamaan (2)

$5a+b-c=-3$

$5\left(1\right)+\left(-5\right)-3=-3$

$5-5-3=-3$

$-3=-3$ (benar)

Pada persamaan (3)

$2a+3b+4c=-1$

$2\left(1\right)+3\left(-5\right)+4\left(3\right)=-1$

$2-15+12=-1$

$-1=-1$ (benar)

maka

$b^2+a-c=\left(-5\right)^2+1-3$

$=25+1-3$

$=23$