Diketahui:
Keliling alas balok 66 cm
Keliling sisi tegak depan 76 cm
Keliling sisi samping kanan 62 cm
Ditanya:
Volume balok =?
Jawab:
Balok tersebut dapat digambarkan seperti berikut.

Persoalan di atas dapat diubah menjadi sistem persamaan linear tiga variabel dan diselesaikan dengan metode eliminasi-substitusi.
Misalkan dalam suatu variabel
Misalkan a= panjang balok, b= lebar balok, dan c= tinggi balok.
Keliling alas balok 66 cm, maka didapatkan persamaan
2(a+b)=66
2a+2b=66
Keliling sisi tegak depan 76 cm, maka didapatkan persamaan
2(a+c)=76
2a+2c=76
Keliling sisi samping kanan 62 cm, maka didapatkan persamaan
2(b+c)=62
2b+2c=62
sehingga diperoleh sistem persamaan linear tiga variabel
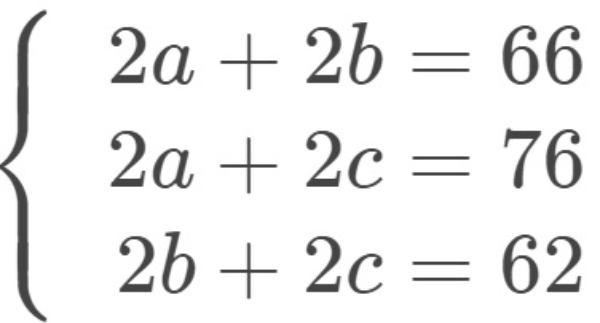
Eliminasikan salah satu variabel dari dua persamaan
Pilih persamaan (1) dan (2) untuk mengeliminasi variabel a sehingga diperoleh
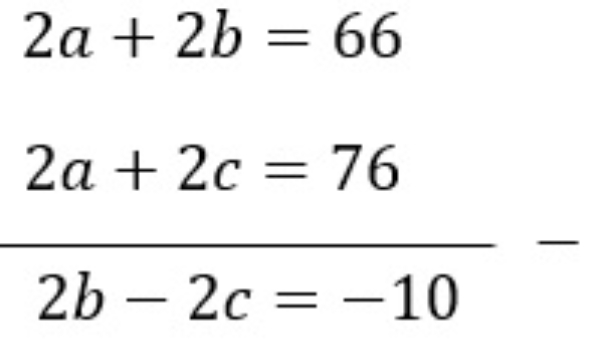
Selesaikan sistem persamaan linear dua variabel yang diperoleh
Diperoleh sistem persamaan linear dua variabel yaitu
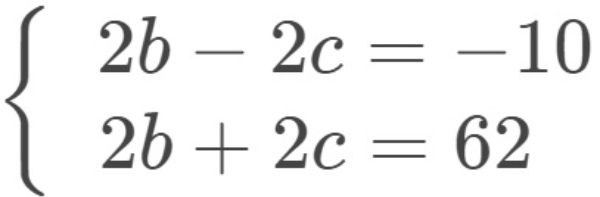
Selesaikan dengan metode eliminasi-substitusi
Proses eliminasi

Proses substitusi
Substitusikan b=13 ke persamaan 2b−2c=−10
2b−2c=−10
2(13)−2c=−10
26−2c=−10
−2c=−36
c=18
Substitusikan c=18 ke persamaan 2a+2c=76
2a+2c=76
2a+2(18)=76
2a+36=76
2a=40
a=20
Periksa nilai penyelesaian
Pada persamaan (1)
2a+2b=66
2(20)+2(13)=66
40+26=66
66=66 (benar)
Pada persamaan (2)
2a+2c=76
2(20)+2(18)=76
40+36=76
76=76 (benar)
Pada persamaan (3)
2b+2c=62
2(13)+2(18)=62
26+36=62
62=62 (benar)
Sehingga diperoleh penyelesaian a=20,b=13,c=18
Maka volume balok adalah
V=a×b×c
=20×13×18
=4.680 cm3