1.
Perhatikan gambar berikut!
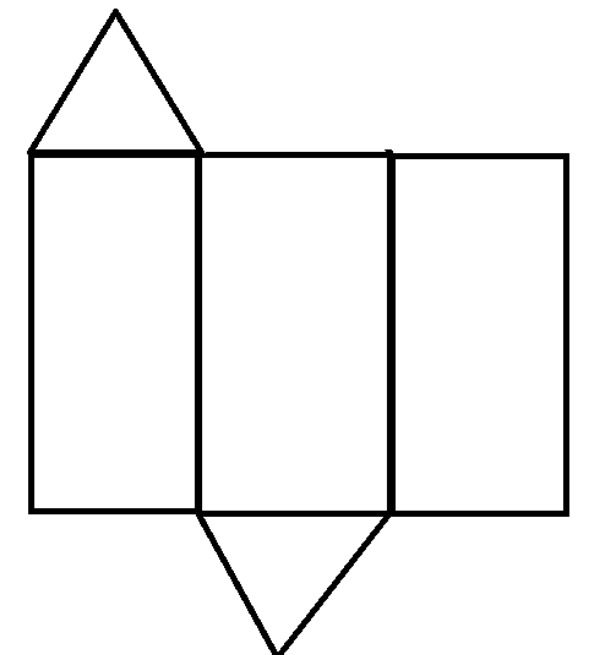
Gambar di samping merupakan jaring-jaring bangun ruang …
Pembahasan:
Gambat tersebut merupakan jaring-jaring bangun prisma (prisma segitiga) karena memiliki bidang alas dan bidang atas yang sejajar dan kongruen/ sebangun.
Pada jaring-jaring tersebut bidang alas dan bidang atas sama-sama berbentuk bangun segitiga.
2.
Bangun ruang yang memiliki 5 titik sudut yaitu bangun …
Pembahasan:
Limas segi empat = 5 titik sudut

Balok = 8 titik sudut

Prisma segitiga = 6 titik sudut

Tabung = tidak memiliki titik sudut

Jawaban yang tepat yaitu limas segiempat
3.
Sebuah prisma segitiga mempunyai sisi sebanyak ... buah.
Pembahasan:
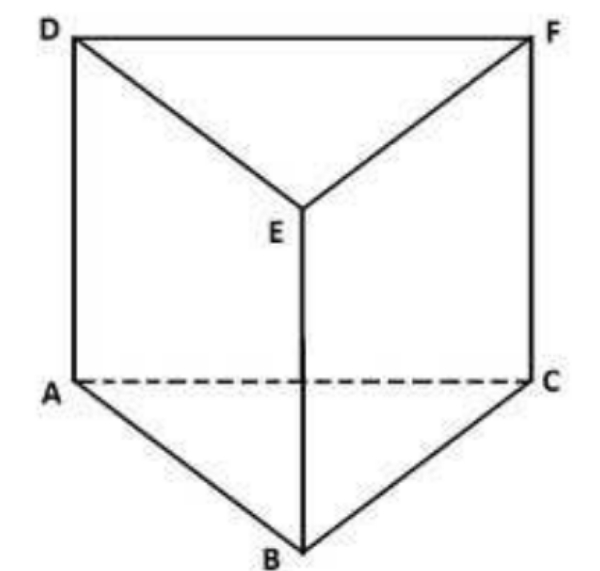
Gambar: Prisma Segitiga
Dari gambar dapat kita lihat bahwa prisma segitiga mempunyai 5 sisi yang terdiri dari:
- 2 sisi berupa segitiga (alas dan atas/tutup)
- 3 sisi berupa segiempat di samping
4.
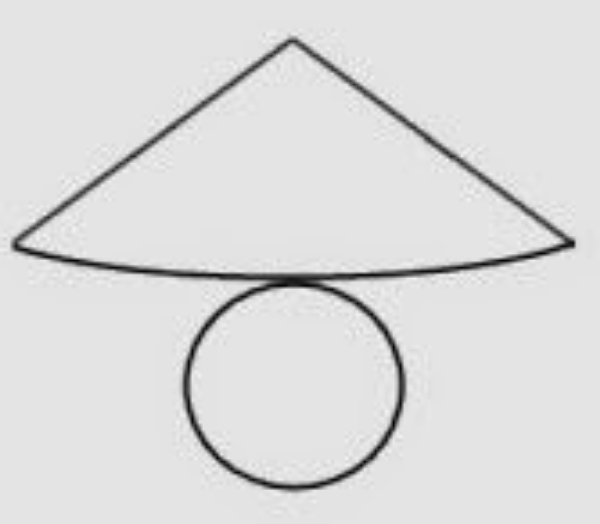
Gambar di atas merupakan jaring-jaring bangun …
Pembahasan:
Jaring-jaring yang terdiri dari satu buah lingkaran (sebagai alas) dan segitiga (sebagai sisi selimut) merupakan salah satu ciri-ciri dari bangun kerucut.
Jika dibentuk menjadi sebuah bangun maka jaring-jaring tersebut akan menjadi bangun ruang: 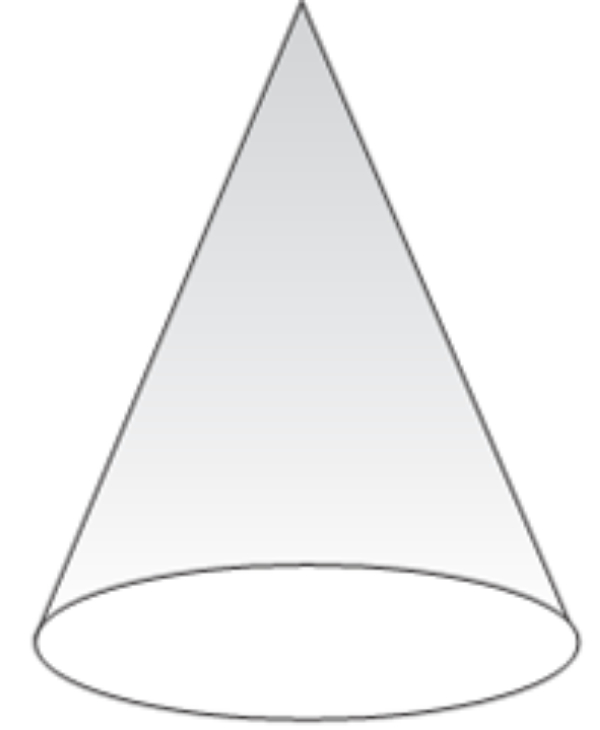
5.
Prisma segitiga ABC.DEF mempunyai tinggi 20 cm. Jika segitiga tersebut mempunyai alas 18 cm dan tinggi 15 cm, maka volume prisma ABC.DEF adalah ... cm3
Pembahasan:
Tinggi prisma = t.prisma = 20 cm
Alas segitiga = a = 18 cm
Tinggi segitiga = t = 15 cm
Volume prisma = Luas alas × tinggi prisma
= 21×a×t× t.prisma
= 21×18×15×20
= 2.700 cm3
6.
Sebuah kerucut mempunyai jari-jari alas 14 cm dan tinggi 15 cm. Volume kerucut tersebut adalah ... cm3.
Pembahasan:
Jari-hari = r = 14 cm
Tinggi kerucut = t = 15 cm
Volume kerucut = 31πr2t
= 31×722×14×14×15
= 3.080 cm3
7.
Sebuah kerucut memiliki luas alas 60 cm2 dan luas selimut 190 cm2. Luas permukaan kerucut tersebut adalah ... cm2
Pembahasan:
Diketahui sebuah kerucut dengan :
Luas alas = 60 cm2
Luas selimut = 190 cm2
Ditanya : Luas permukaan kerucut
Luas permukaan kerucut = luas alas + luas selimut
Luas permukaan kerucut = 60 + 190
Luas permukaan kerucut = 250 cm2
Jadi, luas permukaan kerucut tersebut adalah 250 cm2.
8.
Jari-jari alas sebuah tabung 10 cm dan tingginya 25 cm. luas permukaan tabung adalah … cm2. (π = 722 ) (UASBN 2007/2008)
Pembahasan:
Luas permukaan tabung =
2πr (r + t)
2 x 722 x 10 x (10 + 25)
7440 x 35 = 2.200 cm2
9.
Sebuah kardus berbentuk kubus dengan panjang rusuk 84 cm. Kardus tersebut mampu memuat 392 balok satuan. Panjang balok 21 cm dan lebar 12 cm. Banyak tumpukan satuan dalam kardus adalah ....
Pembahasan:
Langkah I : menghitung volume balok satuan
Panjang rusuk = = 84 cm
Volume kubus = r3=843=592.704 cm3
Banyak balok satuan = 392
Volume balok satuan = 592.704÷392=1.512 cm3
Langkah II : mencari tinggi balok satuan
Balok satuan :
Panjang balok = p = 21 cm
Lebar balok = l = 12 cm
Volume = p×l×t
1.512 = 21×12×t
1.512 = 252×t
t=1.512÷252 = 6 cm
Ukuran balok satuan:
p = 21 cm, l=12 cm, t=6 cm , maka tinggi tumpukan adalah :
= panjang rusuk kubus : tinggi balok satuan
= 84÷6
= 14
10.
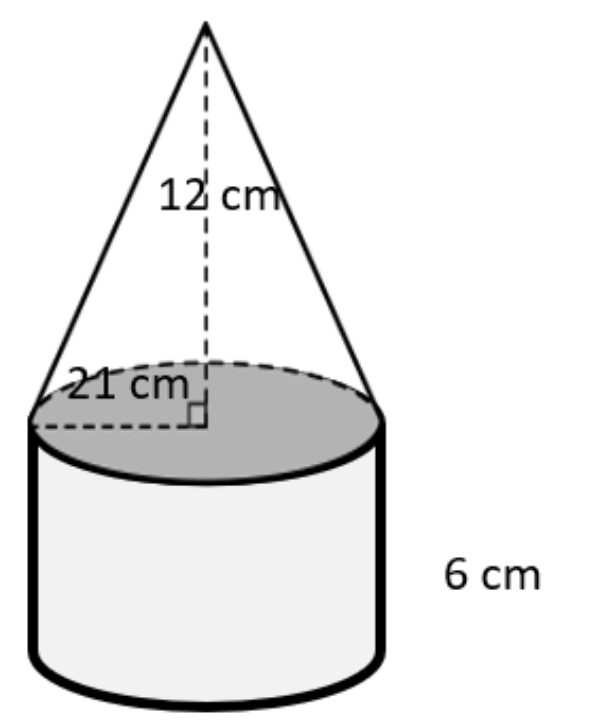
Volume bangun tersebut adalah ... cm3 (Gunakan π = 722)
Pembahasan:
Diketahui sebuah kerucut dan sebuah tabung dengan:
Jari-jari kerucut ( r kerucut ) = jari-jari tabung ( r tabung ) = 21 cm
Tinggi kerucut ( t kerucut ) = 12 cm
Tinggi tabung ( t tabung ) = 6 cm
Ditanya: Volume bangun tersebut
Volume = Volume kerucut + Volume tabung
= 31 × π × ( r kerucut )2 × t kerucut + π × ( r tabung )2 × t tabung
= 31 × 722 × ( 21 )2 × 12 + 722 × ( 21 )2 × 6
= 31 × 722 × 441 × 12 + 722 × 441 × 6
= 5.544 + 8.316
= 13.860 cm3
Jadi, volume bangun tersebut adalah 13.860 cm3.
