1.
Manakah pernyataan di bawah ini tentang kongruen yang benar?
Pembahasan:
Kongruen merupakan keadaan di mana dua bangun datar yang memiliki ukuran sama dan sebangun. Semua bangun datar yang sebangun belum tentu kongruen akan tetapi semua bangun datar yang kongruen sudah dapat dipastikan sebangun.
2.
Perhatikan gambar berikut!
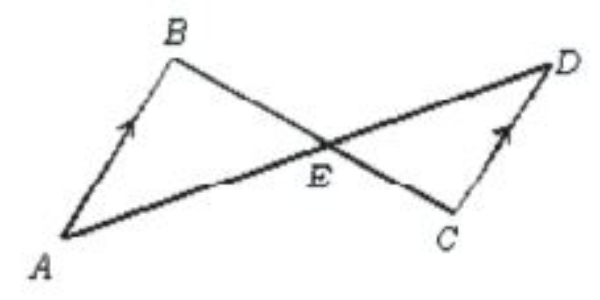
Pada gambar tersebut ΔAEB sebangun dengan ΔCED. Berikut ini yang tidak menyebabkan kedua segitiga tersebut sebangun adalah….
Pembahasan:
Penyelesaian:
Kesebangunan adalah kesamaan perbandingan panjang sisi dan besar sudut antara dua buah bangun datar atau lebih.
Maka, ΔAEB sebangun dengan ΔCED karena

- ∠DCE dan ∠ABE adalah sudut dalam yang bersebrangan
- ∠CED bertolak belakang dengan ∠AEB
- ∠BAE dan ∠DCE sudut dalam bersebrangan
Maka, yang tidak menyebabkan kedua segitiga tersebut sebangun adalah ∠C dan ∠B siku-siku
3.
Perhatikan pernyataan berikut:
i. Dua buah segilima beraturan
ii. Dua buah layang-layang
iii. Dua buah segitiga sama sisi
iv. Dua buah segitiga sama kaki
v. Dua buah jajargenjang persegi
Bangun datar yang sebangun dari pernyataan diatas adalah …
Pembahasan:
Penyelesaian:
Kesebangunan adalah kesamaan perbandingan panjang sisi dan besar sudut antara dua buah bangun datar atau lebih.
Maka, pernyataan yang sebangun adalah i, iii, dan v, karena:
i. dua buah segilima beraturan adalah sebangun, karena memiliki kesamaan perbandingan panjang sisi dan besar sudut
ii. dua buah layang-layang belum tentu sebangun, karena tidak memiliki kesamaan perbandingan panjang sisi dan besar sudut
iii. dua buah segitiga sama sisi adalah sebangun, karena memiliki kesamaan perbandingan panjang sisi dan besar sudut
iv. dua buah segitiga sama kaki belum tentu sebangun, karena tidak memiliki kesamaan perbandingan panjang sisi dan besar sudut
v. dua buah persegi adalah sebangun, karena memiliki kesamaan perbandingan panjang sisi dan besar sudut
4.
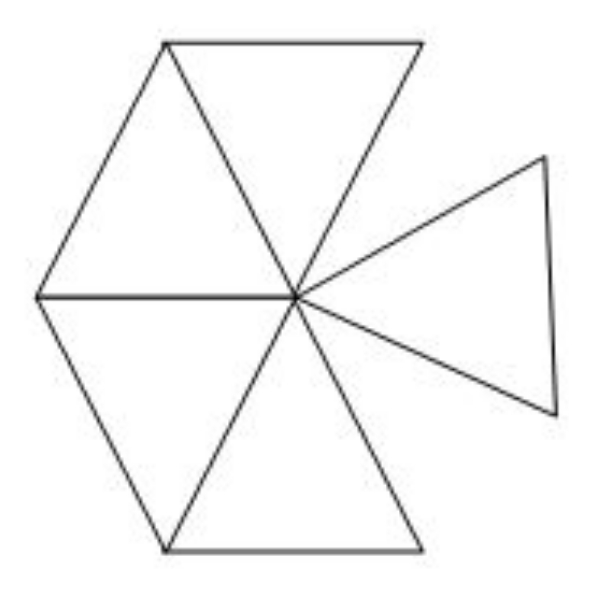
Berdasarkan gambar tersebut, ada berapa banyak segitiga yang kongruen ?
Pembahasan:
Kongruen adalah dua atau lebih benda yang memiliki bentuk dan ukuran yang sama.

Karena pada gambar tersebut terdapat 5 buah segitiga yang memiliki bentuk dan ukuran yang sama, maka 5 buah segitiga tersebut dapat dikatakan kongruen.
Jadi, pada gambar tersebut terdapat 5 segitiga yang kongruen.
5.
ΔPQR sama kaki dengan PQ = QR = 18 cm dan PR = 12 cm. Jika ΔPQR kongruen dengan ΔABC, maka panjang AB adalah ...
Pembahasan:
Diketahui dua buah segitiga sama kaki, ΔPQR kongruen dengan ΔABC, jika digambar:
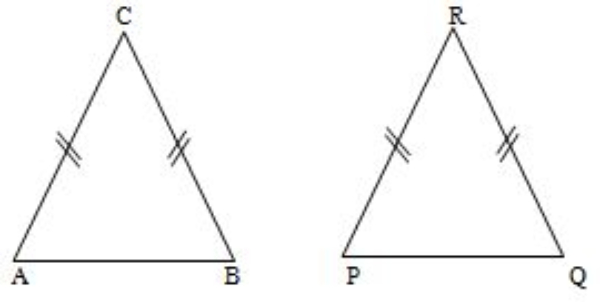
maka:
PQ = AB, PR = AC, dan QR = BC
sehingga:
PR = QR = AC = BC = 18 cm
PQ = AB = 12 cm
Jadi, panjang AB = 12 cm
6.
Perhatikan gambar di bawah ini!
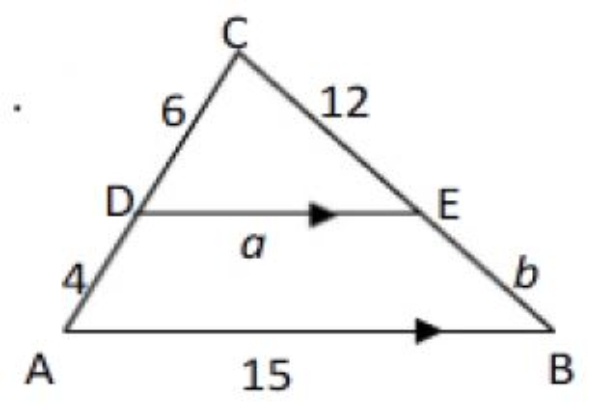
Tentukan panjang a!
Pembahasan:

Diketahui:
AD = 4 cm
CD = 6 cm,
CE = 12 cm
AB = 15 cm
DE = a cm
Ditanya: a?
Dijawab:
Bangun di atas merupakan dua segitiga sebangun.
Maka menurut prinsip kesebangunan:
ACCD=ABDE
⇒AD+DCCD=ABDE
⇒4+66=15a
⇒106=15a
⇒10a=6×15
⇒a=1090
⇒a=9 cm
Jadi, panjang a adalah 9 cm.
7.
Ukuran sebuah mobil panjangnya 3,6 m, lebar 2,4 m dan tinggi 1,8 m. Dibuat model dengan skala 1 :30. Tentukan panjang model!
Pembahasan:
Panjang mobil : 3,6 m = 360 cm
Penyelesaian:
Panjang model : panjang mobil = 1 : 30
Panjang model = 301× panjang mobil
Panjang model = 301×360 cm
Panjang model = 12 cm
Jadi panjang model tersebut adalah 12 cm
8.
Perhatikan gambar di bawah ini!

Panjang DE adalah ....
Pembahasan:
Diketahui:

Ditanya:
Panjang DE=?
Dijawab:
Bangun di atas merupakan △ABC dan △DCE yang sebangun.
Karena sisi-sisi yang bersesuaian mempunyai perbandingan yang sama.
Maka menurut prinsip kesebangunan:
ABDE=ACDC
⇔3DE=412
⇔DE=412×3
⇔DE=3×3
⇔DE=9 cm
Jadi, panjang DE adalah 9 cm.
9.
Segitiga ABC dengan besar ∠A=55o dan ∠B=80o akan sebangun dengan ...
Pembahasan:
Penyelesaian:
∠C = 180o - (∠A + ∠B)
= 180o - (55o + 80o)
= 180o - 135o
= 45o
Untuk mencari segitiga yang sebangun dengan segitiga ABC, kita harus mencari sudut yang bersesuaian dari masing-masing segitiga dengan cara mencari sudut segitiga yang memiliki sudut 55o, 80o, dan 45o.
Maka :
P = 55o, Q = 80o, R = 45o
10.
Ririn mempunyai penggaris segitiga siku-siku. Penggaris tersebut kongruen dengan penggaris Yoga yang memiliki ukuran alas 3 cm dan tinggi 4cm. Sisi miring pada penggaris milik Ririn adalah ....
Pembahasan:
Diketahui:
Dua segitiga siku-siku yang kongruen.
Alas = 3 cm
Tinggi = 4 cm
Ditanya:
Sisi miring pada penggaris Ririn=?
Jawab:

Karena dua penggaris segitiga tersebut kongruen, maka panjang sisi-sisi yang bersesuaian adalah sama:
Alas penggaris Yoga (ay) = alas penggaris Ririn (ar)
Tinggi penggaris Yoga (ty) = Tinggi penggaris Ririn (tr)
Sisi miring penggaris Yoga (my) = sisi miring penggaris Ririn (mr)
Sehingga dengan rumus pythagoras didapatkan
mr=my=(ay)2+(ty)2
mr=my=(3)2+(4)2
mr=my=9+16
mr=my=25
mr=my=5
Jadi, sisi miring pada penggaris milik Ririn adalah 5 cm
