1.
Jaring-jaring di bawah ini merupakan jaring-jaring dari bangun ruang sisi lengkung ....

Pembahasan:
Jaring-jaring sebuah bangun ruang adalah kumpulan beberapa bangun datar yang jika dirangkaikan akan membentuk suatu bangun ruang.
Jaring-jaring pada soal di atas terdiri atas dua buah lingkaran yang mengapit satu buah persegi panjang. Jaring-jaring seperti ini jika dirangkaikan akan membentuk sebuah bangun ruang sisi lengkung tabung. Perhatikan gambar di bawah ini.

Jadi, jaring-jaring yang disajikan pada soal merupakan jaring-jaring dari bangun ruang sisi lengkung tabung.
2.

Sumber Gambar: pinterest.com
Stability ball pada umumnya berbentuk bola. Volume bola adalah ....
Pembahasan:
Volume bola adalah
V=34πr3,
di mana r merupakan jari-jari bola dan nilai π adalah 722 atau 3.14.
3.
Ciri-ciri dari bangun ruang sisi lengkung bola adalah ....
Pembahasan:
Perhatikan gambar bola berikut.

Bola merupakan bangun ruang sisi lengkung yang hanya dibatasi oleh sebuah sisi lengkung, tidak memiliki rusuk, dan juga tidak memiliki titik sudut.
Jadi, ciri-ciri bola adalah memiliki 0 titik sudut, 0 rusuk, dan 1 buah sisi.
4.
Berikut ini merupakan jumlah titik sudut bangun kerucut dan tabung adalah ....
Pembahasan:
Titik sudut adalah titik perpotongan dari dua atau lebih rusuk.
Perhatikan gambar kerucut berikut.

Kerucut hanya memiliki 1 titik sudut yaitu titik perpotongan dua rusuk yang membentuk selimut.
Selanjutnya perhatikan gambar tabung berikut.

Tabung tidak memiliki titik potong antar rusuknya sehingga memiliki 0 titik sudut.
Jadi, jumlah titik sudut bangun kerucut dan tabung adalah 1 dan 0.
5.
Jumlah sisi pada bangun ruang sisi lengkung kerucut, tabung, dan bola berturut-turut adalah ....
Pembahasan:
Kerucut
Bangun ruang sisi lengkung kerucut jika dibongkar akan membentuk jaring-jaring kerucut seperti gambar di bawah ini.

Dari gambar di atas, terlihat bahwa kerucut memiliki satu sisi berbentuk lingkaran sebagai alas dan satu sisi lain yang merupakan selimut kerucut. Jadi, kerucut memiliki 2 buah sisi.
Tabung
Bangun ruang sisi lengkung tabung jika dibongkar akan membentuk jaring-jaring kerucut seperti gambar di bawah ini.

Dari gambar di atas, terlihat bahwa tabung memiliki dua sisi berbentuk lingkaran sebagai alas dan tutupnya, serta satu sisi berbentuk persegi panjang sebagai selimut tabung. Jadi, tabung memiliki 3 buah sisi.
Bola
Perhatikan gambar bola di bawah ini.

Terlihat bahwa bola hanya memiliki satu buah sisi lengkung sebagai permukaannya.
Dengan demikian, jumlah sisi pada bangun ruang sisi lengkung kerucut, tabung, dan bola berturut-turut adalah 2, 3, 1.
6.
Jika volume bola 36π cm3, maka luas kulit bola adalah ... cm2.
Pembahasan:
Diketahui:
Volume bola 36π cm3.
Ditanya:
Luas kulit bola?
Dijawab:
Bola:
volume:
V=34πr3
↔36π=34πr3
↔36=34r3
↔r3=436×3
↔r3=27
↔r3=33
↔r=3 cm.
luas:
L=4πr2
↔L=4×π×32
↔L=4×π×9
↔L=36π cm2.
Jadi, luas kulit bola adalah 36π cm2.
7.
Jika tabung memiliki luas selimut 1.650 cm2 dan tinggi 25 cm, maka jari-jari alas tabung ... cm.
Pembahasan:
Diketahui:
Tabung:
Luas selimut Ls=1.650 cm2 dan tinggi t=25 cm.
Ditanya:
Jari-jari alas tabung?
Dijawab:
Tabung:
Luas selimut:
Ls=2πrt
↔1.650=2×3,14×r×25
↔1.650=50×3,14×r
↔1.650=157×r
↔r=1571.650
↔r=10,5 cm.
Jadi, jari-jari alas tabung 10,5 cm.
Pembahasan:
Kerucut
Kerucut adalah suatu bangun ruang sisi lengkung yang dibatasi oleh dua sisi, yaitu sisi alas dan selimutnya.
Jaring-jaring kerucut adalah gabungan beberapa bangun datar yang jika dirangkai akan membentuk bangun ruang sisi lengkung kerucut.
Berikut jaring-jaring kerucut yang terbentuk jika suatu kerucut dibongkar.

Bola
Bola adalah suatu bangun ruang sisi lengkung yang hanya dibatasi oleh satu sisi lengkung.
Jaring-jaring bola dapat digambarkan seperti punggung buah jeruk. Hal ini karena buah jeruk menyerupai bola, dan jika dibuka tentu akan menyerupai jaring-jaring bola.
Berikut jaring-jaring bola yang terbentuk jika suatu bola dibongkar.

Jadi, jaring-jaring kerucut dan bola ditunjukkan oleh nomor 1 dan 4.
9.

Balon udara berbentuk bola terbuat dari bahan elastis. Bahan yang diperlukan untuk membuat balon udara tersebut jika diameternya 10 m dengan π = 3,14 adalah …
Pembahasan:
Penyelesaian:
Diameter balon udara 10 m, maka r = 5 m
Bahan yang dibutuhkan, artinya luas permukaan bahan. Maka:
L = 4 π r2
L = 4 ×3,14 ×5 m ×5m
L = 314 m2
Jadi, bahan yang dibutuhkan adalah 314 m2
10.
Dalam tabung tertutup terdapat kerucut dan diameter tabung sama dengan tinggi tabung.
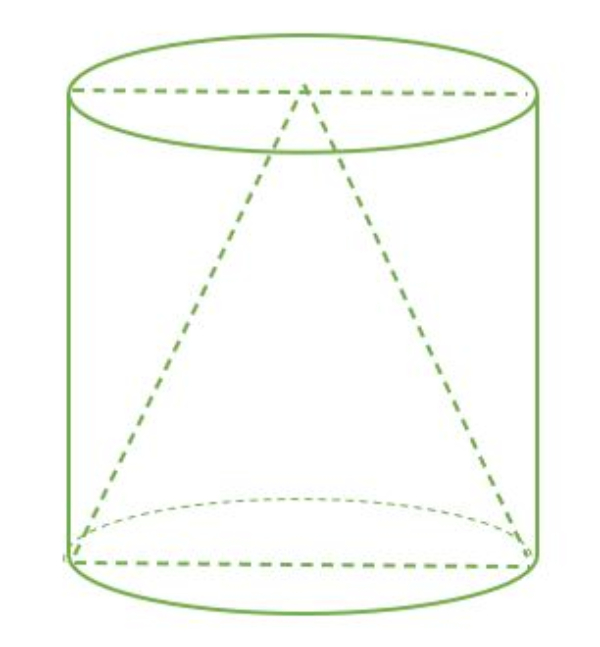
Jika volume kerucut 84 cm3, maka volume tabung ... cm3.
Pembahasan:
Diketahui:
Tabung tertutup terdapat kerucut dan diameter tabung sama dengan tinggi tabung.
Ditanya:
Jika volume kerucut 84 cm3, maka volume tabung?
Dijawab:
Diameter tabung = tinggi tabung
↔d=t
↔2r=t
Kerucut:
Tinggi kerucut = tinggi tabung
Volume:
V=31πr2t
↔V=31πr2(2r)
↔V=32πr3
↔84=32πr3
↔84×3=2πr3
↔252=2πr3
Tabung:
Volume:
V=πr2t
↔V=πr2(2r)
↔V=2πr3
↔252=2πr3
Jadi, volume tabung 252 cm3.
