Pembahasan:
1) Mencari titik potong sumbu- x dan sumbu-y tiap pertidaksamaan



2) Gambar grafik dan menentukan titik-titik pojok
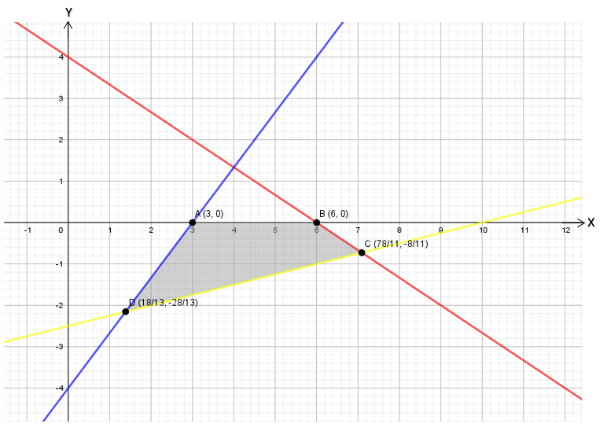
Koordinat di titik C
Mencari nilai y menggunakan metode eliminasi. Pertidaksamaan yang dieliminasi adalah garis merah dengan kuning karena kedua garis tersebut yang saling berpotongan di titik C.
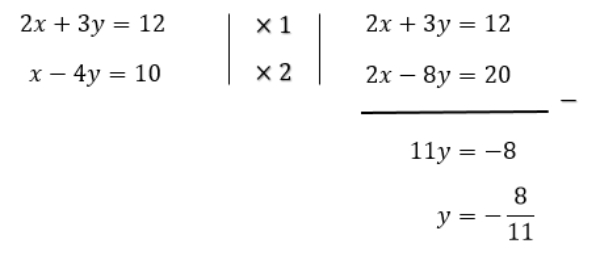
Menentukan nilai x dengan metode subtitusi.
x−4y=10, dengan y=−118
x−4(−118)=10
x=10−1132
x=11110−32
x=1178
Koordinat di titik D
Mencari nilai y menggunakan metode eliminasi. Pertidaksamaan yang dieliminasi adalah garis biru dengan kuning karena kedua garis tersebut yang saling berpotongan di titik D.
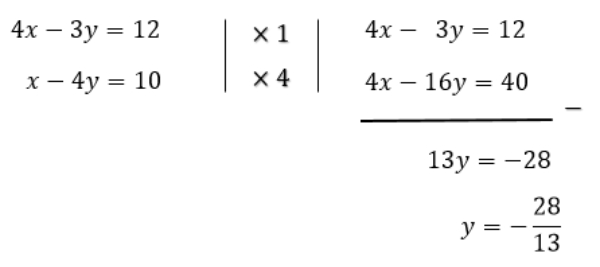
Menentukan nilai x dengan metode substitusi
x−4y=10, dengan y=−1328, maka:
x−4(−1328)=10
x=10−13112=13130−112
x=1318
Titik-titik pojoknya adalah:
A=(3, 0)
B=(6, 0)
C=(1178, −118)
D=(1318, −1328)
3) Nilai Optimum

Jadi, nilai maksimum dari f(x,y)=143x+143y adalah 910
