Pembahasan:
Diketahui: y=−2x3−3x2+1
Ditanya: Interval ketika suatu fungsi selalu naik
Dijawab:
Jika y=h(x)=axn, dimana a,n∈R dan a=0 , maka turunan pertama fungsi h dapat ditentukan dengan metode berikut.
y′=h′(x)=anxn−1
Fungsi dikatakan selalu naik pada interval (m,n) jika memenuhi syarat h′(x)>0. Sebelumnya, kita tentukan terlebih dahulu nilai h′(x)=0, sehingga didapatkan titik stasioner x.
Berdasarkan metode di atas, diperoleh:
y′=h′(x)=(−2×3)x3−1−(3×2)x2−1
h′(x)=−6x2−6x
h′(x)=0
−6x2−6x=0
6x2+6x=0 (Kalikan kedua ruas dengan (−1))
6x(x+1)=0 ⇒ x=−1 atau x=0
Jadi, fungsi h stasioner di titik x=−1 dan x=0.
Nilai h′(x) di sekitar x=−1 dan x=0 disajikan pada gambar di bawah ini.
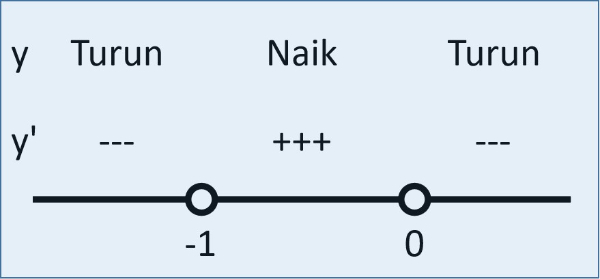
Ambil nilai x=−2 dan substitusikan ke persamaan h′(x).
h′(−2)=−6(−2)2−6(−2)
=−24+12
=−12
Jadi, kurva y=h(x) dikatakan turun pada interval tersebut karena nilai h′(x)<0.
Ambil nilai x=−21 dan substitusikan ke persamaan h′(x).
h′(−2)=−6(−21)2−6(−21)
=−23+3
=23
Jadi, kurva y=h(x) dikatakan naik pada interval tersebut karena nilai h′(x)>0.
Ambil nilai x=1 dan substitusikan ke persamaan h′(x).
h′(1)=−6(1)2−6(1)
=−6−6
=−12
Jadi, kurva y=h(x) dikatakan turun pada interval tersebut karena nilai h′(x)<0.
Jadi, kurva y=h(x)=−2x3−3x2+1 selalu naik pada interval −1<x<0
