Contoh Soal

Pembahasan:

Secara umum bayangan titik $\left(x,y\right)$ yang dirotasikan pada pusat rotasi $O\left(0,0\right)$ dengan sudut rotasi $\theta$ adalah $\left(x',y'\right)$ dengan

Diketahui titik $A\left(x,y\right)$ dirotasi sejauh $-180\degree$ dengan pusat $O\left(0,0\right)$ maka

Jadi, bayangan yang dihasilkan adalah $\left(-x,-y\right)$.

Pembahasan:

Secara umum, bayangan titik $\left(x,y\right)$ oleh refleksi terhadap garis $y=k$ adalah titik $\left(x,2k-y\right)$.

Diketahui pada soal titik $P\left(-1,3\right)$ direfleksikan terhadap garis $y=2.$

Didapat nilai $x=-1,\ y=3,$ dan $k=2$.

Artinya bayangan titik $P\left(-1,3\right)$ oleh refleksi terhadap garis $y=2$ adalah

$\left(x,\ 2k-y\right)=\left(-1,\ 2.2-3\right)=\left(-1,4-3\right)=\left(-1,1\right)$

Pembahasan:

Secara umum bayangan titik $\left(x,y\right)$ yang dirotasikan pada pusat rotasi $\left(a, b\right)$ dengan sudut rotasi $\theta$ adalah $\left(x',y'\right)$ dengan

Diketahui titik $P\left(2,-3\right)$ dirotasi terhadap titik pusat $\left(-2,1\right)$ sebesar $180\degree$maka $x=2,y=-3,a=-2,b=1,\theta=180\degree$

Jadi, bayangan titik yang terbentuk adalah $\left(-6,5\right)$.

Pembahasan:

Secara umum bayangan titik $\left(x,y\right)$ yang didilatasi pada pusat $O\left(0,0\right)$ dengan faktor skala $k$ adalah $\left(x',y'\right)$ dengan

Dimisalkan $\left(x,y\right)$ merupakan titik pada lingkaran $x^2+y^2=16$ dan $\left(x',y'\right)$ merupakan bayangan titik $\left(x,y\right)$ yang didilatasi terhadap pusat $O\left(0,0\right)$ dengan faktor skala $\frac{1}{2}$

Berdasarkan yang diketahui di soal diperoleh $k=\frac{1}{2}$ sehingga

Artinya

$x'=\frac{1}{2}x\ \Rightarrow\ x=2x'$ dan

$y'=\frac{1}{2}y\ \Rightarrow\ y=2y'$

Substitusikan $x=2x'$ dan$\ y=2y'$ pada $x^2+y^2=16$ didapat

$x^2+y^2=16$

$\left(2x'\right)^2+\left(2y'\right)^2=16$

$4\left(x'\right)^2+4\left(y'\right)^2=16$

$\frac{4\left(x'\right)^2+4\left(y'\right)^2}{4}=\frac{16}{4}$

$\left(x'\right)^2+\left(y'\right)^2=4$

Jadi persamaan bayangan lingkaran $x^2+y^2=16$ oleh dilatasi pada pusat $O\left(0,0\right)$ dengan faktor skala $\frac{1}{2}$ adalah

$x^2+y^2=4$

Pembahasan:

Secara umum bayangan suatu titik $A\left(x,y\right)$ yang ditranslasikan oleh  adalah $A'\left(x',y'\right)$ dengan

$x'=x+h$ maka $x=x'-h$

$y'=y+k$ maka $y=y'-k$

Diketahui bahwa $P'\left(2,-15\right)$ hasil translasi oleh . Dengan demikian,

$x'=2,y'=-15,h=3,k=2$

Koordinat titik $P$ adalah

$x=2-3=-1$

$y=-15-2=-17$

Sehingga, $P\left(-1,-17\right)$

Jadi, koordinat titik $P$ adalah $\left(-1,-17\right)$.

Pembahasan:

Diketahui:

$y=x-3$ digeser sejauh $a$ satuan ke kanan dan sejauh $b$ satuan ke bawah

Selanjutnya dirotasi $\left[O,\pi\right]$

Bayangan yang terbentuk adalah $y=x+8$

Ditanya:

Nilai $a-b=?$

Jawab:

Diketahui $y=x-3$ digeser sejauh $a$ satuan ke kanan dan sejauh $b$ satuan ke bawah maka

Selanjutnya dirotasi $\left[O,\pi\right]$ maka

Artinya

$x''=-x-a$ maka $x=-x''-a$

$y''=-y-b$ maka $y=-y''-b$

Substitusikan nilai $x$ dan $y$ ke persamaan $y=x-3$

$y=x-3$

$-y''-b=-x''-a-3$

$-y''=-x''-a-3+b$

Kalikan kedua ruas dengan -1

$y''=x''+a+3-b$

Diketahui hasil bayangan adalah $y=x+8$

Sehingga

$a+3-b=8$

$a-b=8-3$

$a-b=5$

Jadi, nilai $a-b=5$.

Pembahasan:

Perhatikan titik $B$ berikut!

Titik $B$ memiliki koordinat $\left(-3,\ -3\right)$.

Selanjutnya, secara umum bayangan titik $\left(x,\ y\right)$ yang dirotasikan pada pusat rotasi $O\left(0,0\right)$ berturut-turut dengan sudut $\alpha$ dan $\beta$ adalah $\left(x',y'\right)$ dengan

Berdasarkan yang diketahui pada soal diperoleh $x=-3,\ y=-3,\ \alpha=60\degree,$ dan $\beta=120\degree$.

Didapat

Jadi bayangan titik $B$ adalah $\left(3,3\right)$

Pembahasan:

Secara umum, bayangan titik $\left(x,y\right)$ yang dicerminkan (direfleksikan) terhadap sumbu-$X$ adalah $\left(x',y'\right)$$=\left(x,-y\right)$ dengan

Artinya $x'=x$ dan $y'=-y$

Diketahui kurva $y=x^2+3x-2\$ direfleksikan terhadap sumbu-$X$ maka bayangannya

$y=x^2+3x-2\$

$-y'=\left(x'\right)^2+3\left(x'\right)-2$

Kalikan kedua ruas dengan $-1$

$y'=-\left(x'\right)^2-3\left(x'\right)+2$

Jadi, persamaan bayangannya adalah $y=-x^2-3x+2$.

Pembahasan:

Secara umum bayangan titik $\left(x,y\right)$ yang dirotasikan pada pusat rotasi $\left(a, b\right)$ dengan sudut rotasi $\theta$ adalah $\left(x',y'\right)$ dengan

.

Dimisalkan titik $\left(x,y\right)$ berada pada garis $4x-3y-12=0$ dan titik $\left(x',y'\right)$ merupakan bayangan titik $\left(x,y\right)$ oleh rotasi pada pusat $\left(-3, 2\right)$ dengan sudut rotasi $180\degree$.

Artinya $a\ =\ -3,\ b\ =\ 2,$ dan $\theta=180\degree$, sehingga didapat

Artinya

$x'=-x-6\ \Rightarrow\ x=-x'-6$ dan

$y'=-y+4\ \Rightarrow\ y=-y'+4$

Substitusikan $x=-x'-6$ dan $y=-y'+4$ ke dalam $4x-3y-12=0$ diperoleh

$4x-3y-12=0$

$4(-x'-6)-3(-y'+4)-12=0$

$-4x'-24+3y'-12-12=0$

$-4x'+3y'-24-12-12=0$

$-4x'+3y'-48=0$

$-1\left(4x'-3y'+48\right)=-1.0$

$4x'-3y'+48=0$

Jadi bayangan garis $4x-3y-12=0$ oleh rotasi pada pusat rotasi $\left(-3, 2\right)$ dengan sudut rotasi $180\degree$ adalah

$4x-3y+48=0$

Pembahasan:

Secara umum bayangan titik $\left(x,y\right)$ yang dirotasikan pada pusat rotasi $\left(a, b\right)$ dengan sudut rotasi $\theta$ adalah $\left(x',y'\right)$ dengan

.

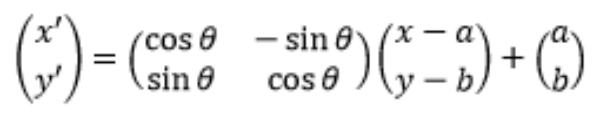Dimisalkan titik $\left(x,y\right)$ berada pada parabola $y=x^2+10x+27$ dan titik $\left(x',y'\right)$ merupakan bayangan titik $\left(x,y\right)$ oleh rotasi pada pusat $\left(1, -1\right)$ dengan sudut rotasi $-180\degree$.

Artinya $a=1,\ b=-1,$ dan $\theta=-180\degree$, sehingga didapat

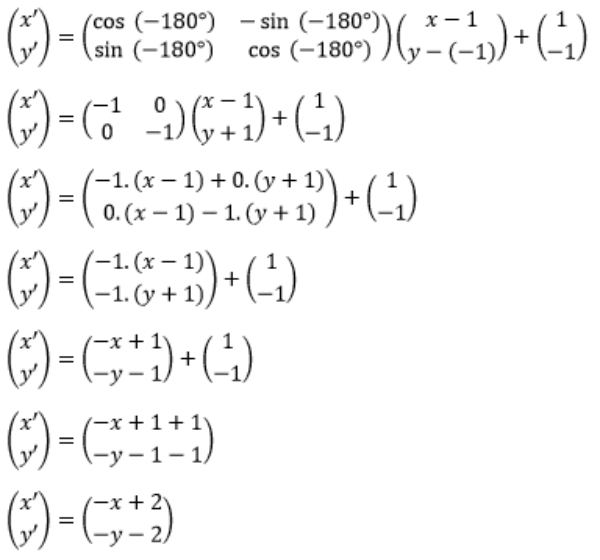
Artinya

$x'=-x+2\ \Rightarrow\ x=-x'+2$ dan

$y'=-y-2\ \Rightarrow\ y=-y'-2$

Substitusikan $x=-x'+2$ dan $y=-y'-2$ ke dalam $y=x^2+10x+27$ diperoleh

$y=x^2+10x+27$

$-y'-2=(-x'+2)^2+10(-x'+2)+27$

$-y'-2=(x')^2-4x'+4-10x'+20+27$

$-y'-2=(x')^2-4x'-10x'+4+20+27$

$-y'-2=(x')^2-14x'+51$

$-y'=(x')^2-14x'+51+2$

$-y'=(x')^2-14x'+53$

Jadi bayangan parabola $y=x^2+10x+27$ oleh rotasi pada pusat rotasi $\left(1, -1\right)$ dengan sudut rotasi $-180\degree$adalah

$-y=x^2-14x+53$