Pembahasan:
Diketahui:
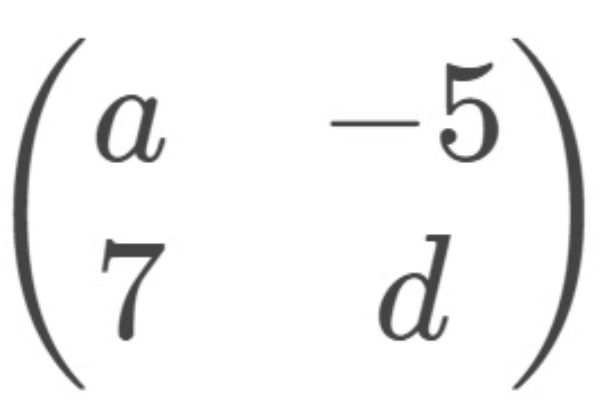 +
+ 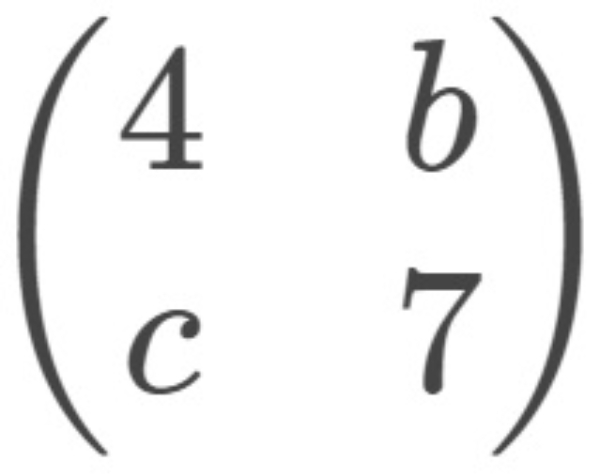 =
= 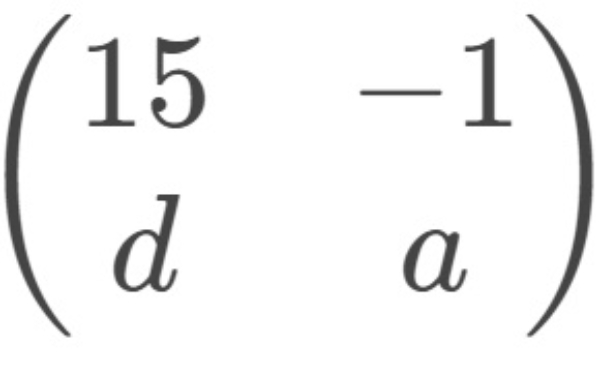 −
− 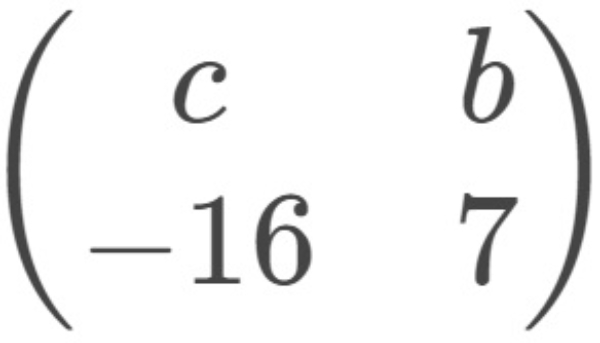
Ditanya:
a+b+c+d=
Jawab:
Jika A = 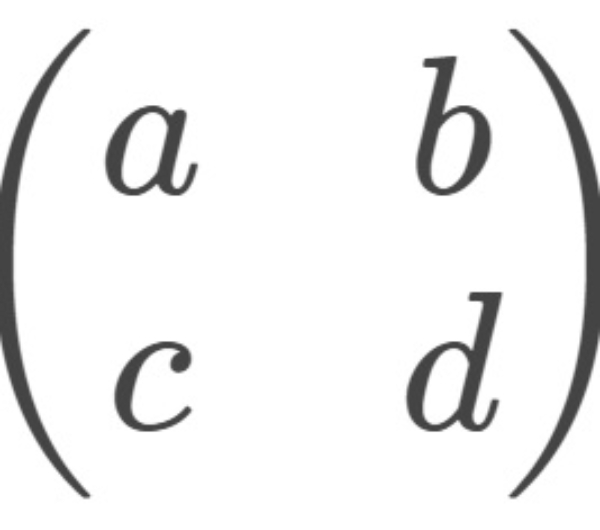 dan B =
dan B = 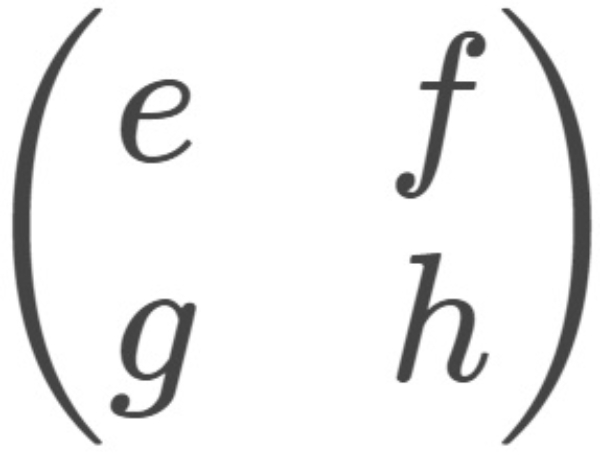
Rumus umum penjumlahan dua matriks adalah
A+B= 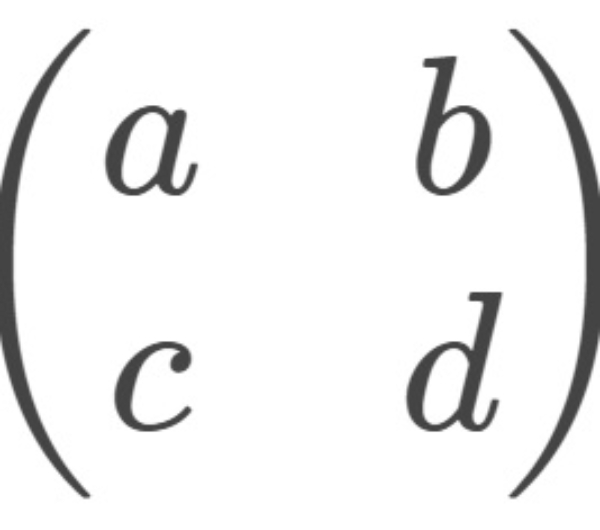 +
+ 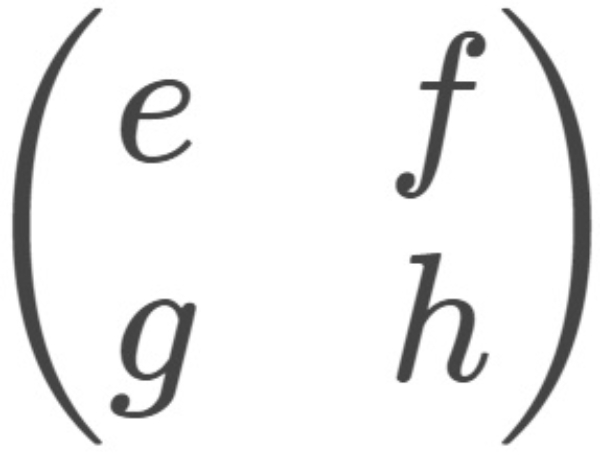
= 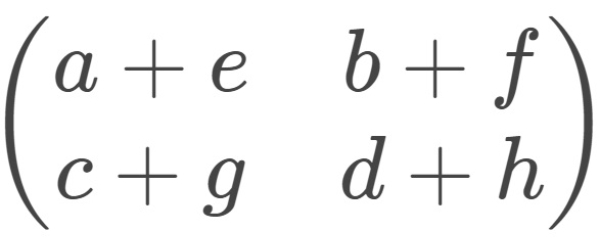
Rumus umum pengurangan dua matriks adalah
A−B= 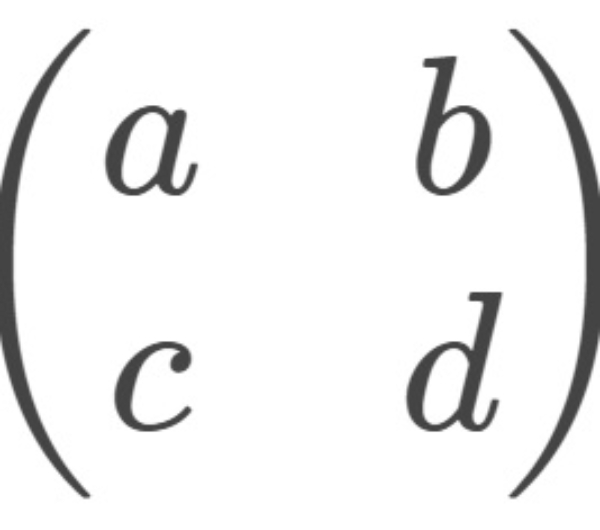 −
− 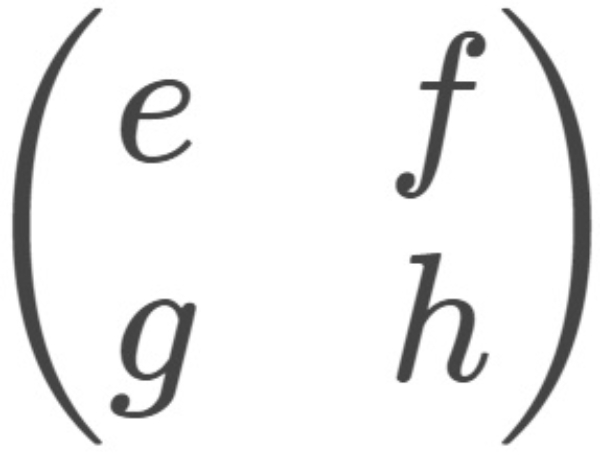
= 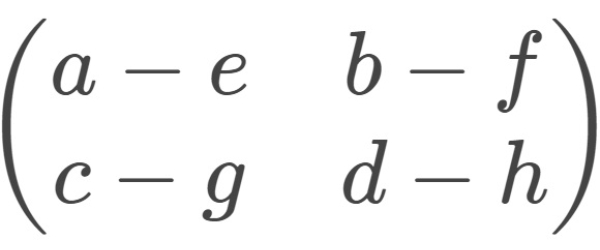
Dengan demikian
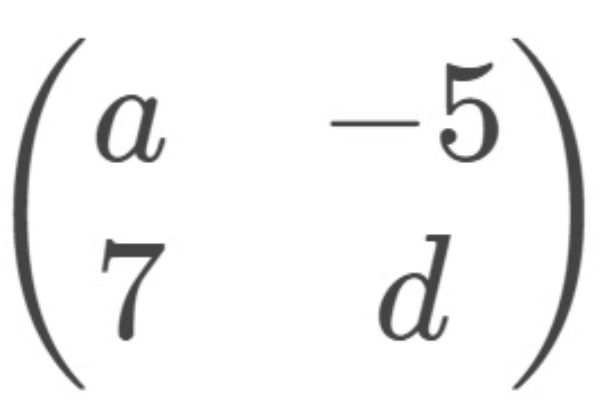 +
+ 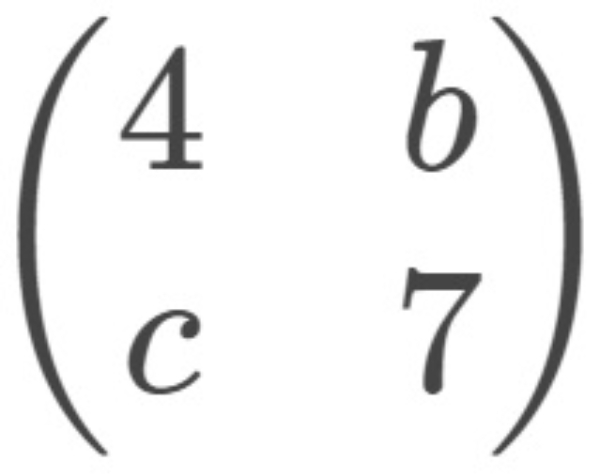 =
= 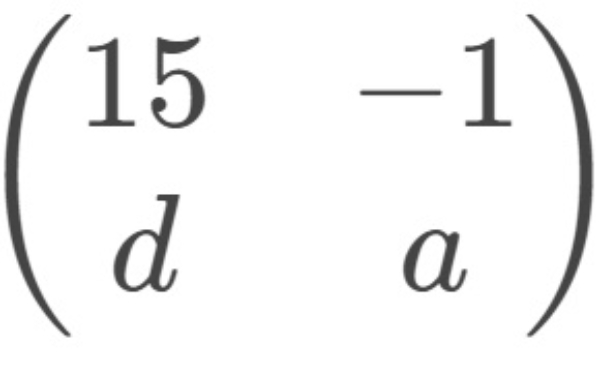 −
− 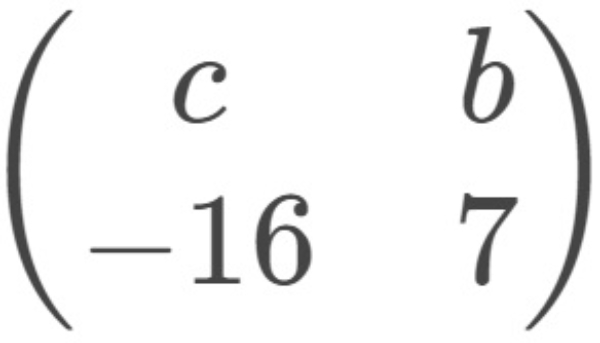
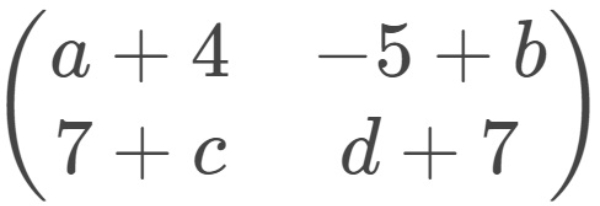 =
= 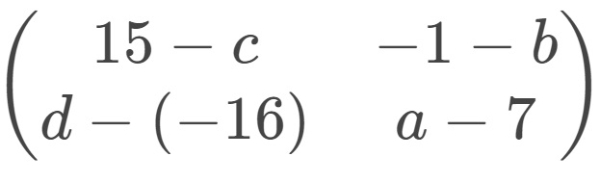
diperoleh persamaan
a+4=15−c ..... (1)
−5+b=−1−b ..... (2)
7+c=d+16 .....(3)
d+7=a−7 ..... (4)
dari persamaan (2) didapatkan
−5+b=−1−b
b+b=−1+5
2b=4
b=2
persamaan (3) dan (4) dapat dituliskan
7+c=d+16 .....(3)
c−d=16−7 .....(3)
c−d=9 .....(3)
d+7=a−7 .....(4)
d−a=−7−7 .....(4)
d−a=−14.....(4)
Eliminasi persamaan (3) dan (4)
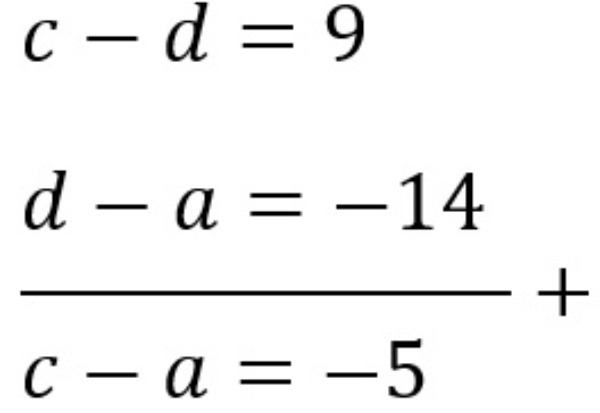
persamaan (1) dapat dituliskan
a+4=15−c .....(1)
a+c=15−4 ..... (1)
a+c=11 .... (1)
eliminasi persamaan (5) dan (1)
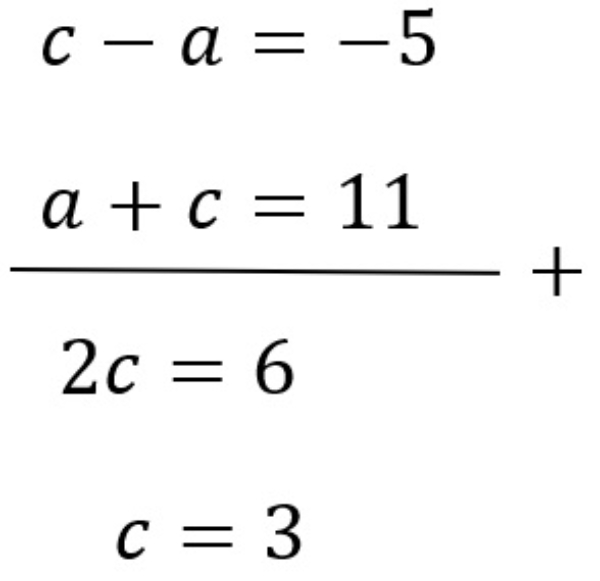
Substitusikan c=3 pada persamaan (1)
a+c=11
a+3=11
a=11−3
a=8
Substitusikan c=3 pada persamaan (3)
c−d=9
3−d=9
−d=9−3
−d=6
d=−6
diperoleh a=8, b=2, c=3, d=−6
maka
a+b+c+d=8+2+3+(−6)
a+b+c+d=7
