Contoh Soal

Pembahasan:

Diketahui:

Kurva $f(x)=2\sin x\cos x$

Ditanya:

Gradien garis singgung kurva $f(x)=2\sin x\cos x$ di absis $x=\frac{\pi}{6}$ ?

Jawab:

Nilai kemiringan / gradien garis singgung suatu kurva $f\left(x\right)$ dapat dicari menggunakan turunan yaitu

$m=f'\left(x\right)=\lim_{h\to0}\frac{f\left(x+h\right)-f\left(x\right)}{h}$

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sin x$ turunannya adalah $y'=\cos x$

Untuk fungsi $y=\cos x$ turunannya adalah $y'=-\sin x$

Untuk fungsi $y=u.v$ turunannya adalah $y'=u'v+uv'$

Dengan demikian, akan dicari turunan pertama dari kurva $f(x)=2\sin x\cos x$

Kurva yang diketahui pada soal berbentuk $f(x)=u.v$ dengan $u=2\sin x$ dan $v=\cos x$

Diperoleh

$u'=2\cos x$

$v'=-\sin x$

$f'(x)=u'v+uv'$

$\Leftrightarrow f'(x)=2\cos x\cos x+2\sin x(-\sin x)$

$\Leftrightarrow f'(x)=2\cos^2 x-2\sin^2 x$

$\Leftrightarrow f'(x)=2\left(\cos^2x-\sin^2x\right)$

Perlu diingat bahwa $\cos^2x-\sin^2x=\cos2x$ sehingga didapat

$f'(x)=2\cos2x$

Selanjutnya gradien garis singgung kurva $f(x)=2\sin x\cos x$ di absis $x=\frac{\pi}{6}$adalah

$m=f'(\frac{\pi}{6})=2\cos2\frac{\pi}{6}$

$\Leftrightarrow m=2\cos\frac{\pi}{3}$

$\Leftrightarrow m=2.\frac{1}{2}$

$\Leftrightarrow m=1$

Pembahasan:

Diketahui:

Fungsi $y=\cos x-17$ dengan $0\degree\le x\le360\degree$

Ditanya:

Subinterval di dalam $0\degree\le x\le360\degree$ yang membuat kurva $y$ selalu turun?

Jawab:

Diberikan fungsi $y=f\left(x\right)$ dalam interval $I$ dengan $f\left(x\right)$ diferensiabel untuk setiap $x\in I$ berlaku

1. jika $f'\left(x\right)>0$ untuk setiap $x\in I$, maka kurva $f\left(x\right)$ selalu naik pada interval $I$
2. jika $f'\left(x\right)<0$ untuk setiap $x\in I$, maka kurva $f\left(x\right)$ selalu turun pada interval $I$
3. jika $f'\left(x\right)=0$ untuk setiap $x\in I$, maka kurva $f\left(x\right)$ stasioner (diam) pada interval $I$
4. jika $f'\left(x\right)\ge0$ untuk setiap $x\in I$, maka kurva $f\left(x\right)$ tidak pernah turun pada interval $I$
5. jika $f'\left(x\right)\le0$ untuk setiap $x\in I$, maka kurva $f\left(x\right)$ tidak pernah naik pada interval $I$

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\cos x$ turunannya adalah $y'=-\sin x$

Untuk fungsi $y=a$ dengan $a$ suatu konstanta turunannya adalah $y'=0$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Pada soal diketahui fungsi $y=\cos x-17$ dengan $0\degree\le x\le360\degree$. Turunan pertamanya adalah $y'=-\sin x$. Pembuat nol dari $y'$ adalah

$y'=0$

$\Leftrightarrow-\sin x=0$

$\Leftrightarrow\sin x=\sin0\degree$

Perlu diingat bahwa penyelesaian persamaan $\sin\left(ax+b\right)=\sin\theta$ adalah $ax+b=\theta+k.360\degree$ atau $ax+b=\left(180\degree-\theta\right)+k.360\degree$ sehingga untuk $\sin x=\sin0$ didapat

$x=0\degree+k.360\degree=k.360\degree$

untuk $k=0$ didapat $x=0.360\degree=0\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=1$ didapat $x=1.360\degree=360\degree$ memenuhi $0\degree\le x\le360\degree$

atau

$x=\left(180\degree-0\degree\right)+k.360\degree=180\degree+k.360\degree$

untuk $k=0$ didapat $x=180\degree+0.360\degree=180\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=1$ didapat $x=180\degree+1.360\degree=540\degree$ tidak memenuhi $0\degree\le x\le360\degree$

Artinya, pembuat nol dari $y'$ adalah $x=\left\{0\degree, 180\degree, 360\degree\right\}$. Selanjutnya, cek nilai dari $y'$ untuk setiap subinterval yang terbentuk.

Untuk subinterval $0\degree\le x<180\degree$ dipilih $x=90\degree$ didapat

$y'=-\sin 90\degree=-1$ (negatif).

Untuk subinterval yang lain dicari dengan cara yang sama, sehingga diperoleh

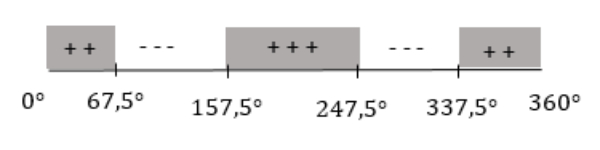
yang diminta pada soal subinterval yang membuat kurva $y$ selalu turun atau dengan kata lain $y'<0$ (negatif). Kemudian akan dicari nilai $y'$ untuk $x=0\degree$ dan $x=360\degree$ didapat

$y'=-\sin 0\degree=0$ (netral)

$y'=-\sin 360\degree=0$ (netral)

Jadi subinterval di dalam $0\degree\le x\le360\degree$ yang membuat kurva $y=\cos x-17$ selalu turun adalah $0\degree< x<180\degree$

Pembahasan:

Diketahui:

Ekspresi implisit $\tan(x-y)=2x+3y^2$

Ditanya:

Turunan pertama terhadap $x$ dari ekspresi implisit $\tan(x-y)=2x+3y^2$ ?

Jawab:

Secara umum, untuk menentukan turunan pertama suatu ekspresi implisit menggunakan aturan rantai, yaitu:

Jika $y=f\left(t\right)$ dan $t=g\left(x\right)$ sehingga $y=h\left(x\right)=f\left(g\left(x\right)\right)$ maka turunan pertamanya adalah

$y'=h'\left(x\right)=f'\left(g\left(x\right)\right)g'\left(x\right)$

atau

$\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$

Perhatikan ruas kiri ekspresi implisit yang diketahui pada soal, yaitu $\tan\left(x-y\right)$

Misalkan $t=x-y$ dan $y$ dalam $x$ (atau $y=f\left(x\right)$ ). Akibatnya $\tan\left(x-y\right)=\tan t$

Akan dicari turunan pertama $\tan\left(x-y\right)$ terhadap $x$ menggunakan aturan rantai. Diperoleh

Turunan pertama $\tan\left(x-y\right)=\tan t$ terhadap $t$ adalah $\sec^2t=\sec^2(x-y)$

Turunan pertama $t=x-y$ terhadap $x$ adalah $1-\frac{dy}{dx}$

Dengan demikian turunan pertama $\tan\left(x-y\right)$ terhadap $x$ adalah

$\sec^2(x-y)\left(1-\frac{dy}{dx}\right)=\sec^2(x-y)-\sec^2(x-y)\frac{dy}{dx}$

Selanjutnya perhatikan ruas kanan ekspresi implisit yang diketahui pada soal, yaitu $2x+3y^2$. Karena $y$ dalam $x$ (atau $y=f\left(x\right)$ ), maka dengan menggunakan aturan rantai, turunan pertama dari $2x+3y^2$ adalah $2+3.2y\frac{dy}{dx}=2+6y\frac{dy}{dx}$

Berdasarkan turunan ruas kiri dan turunan ruas kanan yang sudah diperoleh sebelumnya, didapat

$\sec^2(x-y)-\sec^2(x-y)\frac{dy}{dx}=2+6y\frac{dy}{dx}$

$\Leftrightarrow\sec^2(x-y)-2=6y\frac{dy}{dx}+\sec^2(x-y)\frac{dy}{dx}$

$\Leftrightarrow\sec^2(x-y)-2=(6y+\sec^2(x-y))\frac{dy}{dx}$

$\Leftrightarrow\frac{\sec^2(x-y)-2}{6y+\sec^2(x-y)}=\frac{dy}{dx}$

Pembahasan:

Diketahui:

Fungsi $f\left(x\right)=\sqrt{8}\sin x+\cos x$ dengan $0\le x\le2\pi$

Ditanya:

Nilai stasioner dari fungsi $f\left(x\right)=\sqrt{8}\sin x+\cos x$ ?

Jawab:

Secara umum nilai stasioner adalah nilai $f\left(x\right)$ ketika $f'\left(x\right)=0$. Dengan demikian untuk mencari nilai stasioner terlebih dahulu dicari pembuat nol untuk $f'\left(x\right)$.

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sin x$ turunannya adalah $y'=\cos x$

Untuk fungsi $y=\cos x$ turunannya adalah $y'=-\sin x$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Pada soal diketahui fungsi $f\left(x\right)=\sqrt{8}\sin x+\cos x$. Diperoleh

$f'\left(x\right)=\sqrt{8}\cos x-\sin x$

dengan pembuat nol

$f'\left(x\right)=0$

$\Leftrightarrow\sqrt{8}\cos x-\sin x=0$

$\Leftrightarrow\sqrt{8}\cos x=\sin x$

$\Leftrightarrow\sqrt{8}=\frac{\sin x}{\cos x}$

$\Leftrightarrow\sqrt{8}=\tan x$

Perlu diingat pembagian kuadran sebagai berikut:

dan nilai $\sin\theta,\ \cos\theta,$ dan $\tan\theta$ yang positif pada setiap kuadran adalah

Sebelumnya telah diperoleh $\tan x=\sqrt{8}$ (positif) artinya $x$ berada di kuadran I atau III.

Perlu diingat bahwa nilai $\sin\theta,\ \cos\theta,$ dan $\tan\theta$ dapat dinyatakan dalam segitiga siku-siku, yaitu

Sebelumnya telah diperoleh $\tan x=\sqrt{8}$, dengan menggunakan Teorema Pythagoras diperoleh

Dengan mengingat nilai positif atau negatif untuk setiap kuadran. Untuk kuadran I diperoleh $\sin x=\frac{\sqrt{8}}{3}$ dan $\cos x=\frac{1}{3}$ sehingga

$f\left(x\right)=\sqrt{8}\sin x+\cos x$

$\Leftrightarrow f\left(x\right)=\sqrt{8}.\frac{\sqrt{8}}{3}+\frac{1}{3}$

$\Leftrightarrow f\left(x\right)=\frac{8}{3}+\frac{1}{3}$

$\Leftrightarrow f\left(x\right)=\frac{9}{3}$

$\Leftrightarrow f\left(x\right)=3$

Untuk kuadran III, diperoleh $\sin x=-\frac{\sqrt{8}}{3}$ dan $\cos x=-\frac{1}{3}$ sehingga

$f\left(x\right)=\sqrt{8}\sin x+\cos x$

$\Leftrightarrow f\left(x\right)=\sqrt{8}.\left(-\frac{\sqrt{8}}{3}\right)+\left(-\frac{1}{3}\right)$

$\Leftrightarrow f\left(x\right)=-\frac{8}{3}-\frac{1}{3}$

$\Leftrightarrow f\left(x\right)=-\frac{9}{3}$

$\Leftrightarrow f\left(x\right)=-3$

Jadi, titik stasioner dari fungsi $f\left(x\right)=\sqrt{8}\sin x+\cos x$ adalah $3$ dan $-3$

Pembahasan:

Diketahui:

Suatu benda memiliki kecepatan $v\left(x\right)=\cos 2x+2$ m/s

Ditanya:

Kecepatan minimum benda tersebut?

Jawab:

Mencari kecepatan minimum dapat dilakukan dengan mencari nilai minimum dari fungsi kecepatannya.

Perlu diingat untuk sembarang fungsi $f\left(x\right)$ dan titik $x=a$ berlaku

1. ketika $f'\left(a\right)=0$ dan $f''\left(a\right)>0$ maka $f\left(a\right)$ merupakan nilai minimum
2. ketika $f'\left(a\right)=0$ dan $f''\left(a\right)<0$ maka $f\left(a\right)$ merupakan nilai maksimum
3. ketika $f'\left(a\right)=0$ dan $f''\left(a\right)=0$ maka $f\left(a\right)$ bukan nilai ekstrim (minimum maupun maksimum).

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sin x$ turunannya adalah $y'=\cos x$

Untuk fungsi $y=\cos x$ turunannya adalah $y'=-\sin x$

Untuk fungsi $y=a$ dengan $a$ suatu konstanta turunannya adalah $y'=0$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Diketahui fungsi kecepatannya adalah $v\left(x\right)=\cos 2x+2$ sehingga didapat

$v'\left(x\right)=-2\sin 2x$

Perlu diingat bahwa turunan kedua suatu fungsi diperoleh dengan mencari turunan pertama dari turunan pertama fungsi tersebut. Diperoleh

$v''\left(x\right)=-4\cos 2x$

Syarat pertama untuk mencari nilai minimum suatu fungsi adalah dengan mencari pembuat nol turunan pertamanya. Didapat

$v'\left(x\right)=0$

$\Leftrightarrow-2\sin 2x=0$

$\Leftrightarrow\sin 2x=\sin 0\degree$

sebab $\sin 0\degree=0$

Perlu diingat bahwa penyelesaian persamaan $\sin\left(ax+b\right)=\sin\theta$ adalah $ax+b=\theta+k.360\degree$ atau $ax+b=\left(180\degree-\theta\right)+k.360\degree$ sehingga untuk $\sin 2x=\sin 0\degree$ didapat

$2x=0\degree+k.360\degree$

$\Leftrightarrow x=k.180\degree$

untuk $k=0$ maka $x=0.180\degree=0\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=1$ maka $x=1.180\degree=180\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=2$ maka $x=2.180\degree=360\degree$ memenuhi $0\degree\le x\le360\degree$

atau

$2x=180\degree-0\degree+k.360\degree$

$\Leftrightarrow x=90\degree+k.180\degree$

untuk $k=0$ maka $x=90\degree+0.180\degree=90\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=1$ maka $x=90\degree+1.180\degree=270\degree$ memenuhi $0\degree\le x\le360\degree$

untuk $k=2$ maka $x=90\degree+2.180\degree=450\degree$ tidak memenuhi $0\degree\le x\le360\degree$

Selanjutnya, diperhatikan nilai turunan kedua untuk setiap $x$ yang diperoleh

$v''\left(0\degree\right)=-4\cos (2.0\degree)=-4\cos (0\degree)=-4<0$ (maksimum)

$v''\left(90\degree\right)=-4\cos (2.90\degree)=-4\cos (180\degree)=4>0$ (minimum)

$v''\left(180\degree\right)=-4\cos (2.180\degree)=-4\cos (360\degree)=-4<0$ (maksimum)

$v''\left(270\degree\right)=-4\cos (2.270\degree)=-4\cos (180\degree)=4>0$ (minimum)

$v''\left(360\degree\right)=-4\cos (2.360\degree)=-4\cos (360\degree)=-4<0$ (maksimum)

Artinya $v\left(90\degree\right)=\cos (2.90\degree)+2=\cos (180\degree)+2=-1+2=1$ adalah nilai minimum fungsi kecepatan kecepatan $v\left(x\right)=\cos 2x+2$. Jadi kecepatan minimumnya adalah 1 m/s

Pembahasan:

Diketahui:

Fungsi $f(x)=3\sec x\cot x$ dan kurva $y=f\left(x\right)$

Ditanya:

Persamaan garis singgung pada kurva $y=f\left(x\right)$ di titik $(30\degree, 6)$ ?

Jawab:

Nilai kemiringan / gradien garis singgung suatu kurva $f\left(x\right)$ dapat dicari menggunakan turunan yaitu

$m=f'\left(x\right)=\lim_{h\to0}\frac{f\left(x+h\right)-f\left(x\right)}{h}$

sehingga persamaan garis singgung pada kurva $f\left(x\right)$ di titik $\left(x_1,\ y_1\right)$ adalah

$y-y_1=f'\left(x_1\right)\left(x-x_1\right)$

Pertama akan dicari turunan pertama fungsi $f\left(x\right)$.

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sec x$ turunannya adalah $y'=\sec x\tan x$

Untuk fungsi $y=\cot x$ turunannya adalah $y'=-\csc^2 x$

Untuk fungsi $y=u.v$ turunannya adalah $y'=u'v+uv'$

Kurva yang diketahui pada soal berbentuk $g(x)=u.v$ dengan $u=3\sec x$ dan $v=\cot x$

Diperoleh

$u'=3\sec x\tan x$

$v'=-\csc^2 x$

Dengan demikian

$f'\left(x\right)=u'v+uv'$

$\Leftrightarrow f'\left(x\right)=3\sec x\tan x\cot x+3\sec x(-\csc^2 x)$

$\Leftrightarrow f'\left(x\right)=3\sec x\tan x\cot x-3\sec x\csc^2 x$

Perlu diingat bahwa $\tan x\cot x=1$, $\sec x=\frac{1}{\cos x}$, dan $\csc x=\frac{1}{\sin x}$, sehingga didapat

$f'\left(x\right)=3\sec x(1-\csc^2 x)$

$\Leftrightarrow f'\left(x\right)=3\frac{1}{\cos x}(1-\frac{1}{\sin^2 x})$

dan gradien garis singgung pada kurva $y=f\left(x\right)$ di titik $(30\degree, 6)$ adalah

$m=f'\left(30\degree\right)$

$\Leftrightarrow m=3\frac{1}{\cos 30\degree}(1-\frac{1}{\sin^2 30\degree})$

$\Leftrightarrow m=3\frac{1}{\frac{1}{2}\sqrt3}(1-\frac{1}{(\frac{1}{2})^2})$

$\Leftrightarrow m=3\frac{2\sqrt3}{\sqrt3\sqrt3}(1-\frac{1}{\frac{1}{4}})$

$\Leftrightarrow m=2\sqrt3(1-4)$

$\Leftrightarrow m=2\sqrt3(-3)$

$\Leftrightarrow m=-6\sqrt3$

Selanjutnya persamaan garis singgung pada kurva $y=f\left(x\right)$ di titik $(30\degree, 6)$ adalah

$y-6=-6\sqrt3\left(x-30\degree\right)$

$\Leftrightarrow y=-6\sqrt3\left(x-30\degree\right)+6$

Pembahasan:

Diketahui:

Fungsi $y=\frac{\tan x}{\cos x}$

Ditanya:

Turunan pertama dari $y=\frac{\tan x}{\cos x}$ ?

Jawab:

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\tan x$ turunannya adalah $y'=\sec^2 x$

Untuk fungsi $y=\cos x$ turunannya adalah $y'=-\sin x$

Untuk fungsi $y=\frac{u}{v}$ turunannya adalah $y'=\frac{u'v-uv'}{v^2}$

Fungsi yang diketahui pada soal berbentuk $y=\frac{u}{v}$ dengan $u=\tan x$ dan $v=\cos x$

Diperoleh

$u'=\sec^2x$

$v'=-\sin x$

Perlu diingat bahwa $\sec x=\frac{1}{\cos x}$ dan $\tan x=\frac{\sin x}{\cos x}$

Dengan demikian didapat

$y'=\frac{u'v-uv'}{v^2}$

$\Leftrightarrow y'=\frac{\sec^2x\cos x-\tan x\left(-\sin x\right)}{\cos^2x}$

$\Leftrightarrow y'=\frac{\frac{1}{\cos^2x}\cos x-\frac{\sin x}{\cos x}\left(-\sin x\right)}{\cos^2x}$

$\Leftrightarrow y'=\frac{\frac{1}{\cos x}+\frac{\sin^2x}{\cos x}}{\cos^2x}$

$\Leftrightarrow y'=\frac{\frac{1+\sin^2x}{\cos x}}{\cos^2x}$

$\Leftrightarrow y'=\frac{1+\sin^2x}{\cos^3x}$

Pembahasan:

Diketahui:

Fungsi $f(x)=5\sec x-3\csc x+2x$

Ditanya:

Turunan pertama dari $f(x)=5\sec x-3\csc x+2x$ ?

Jawab:

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=\sec x$ turunannya adalah $y'=\sec x\tan x$

Untuk fungsi $y=\csc x$ turunannya adalah $y'=-\csc x\cot x$

Untuk fungsi $y=x^n$ turunannya adalah $y'=nx^{n-1}$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Fungsi yang diketahui pada soal berbentuk $f\left(x\right)=f_1\left(x\right)+f_2\left(x\right)+f_3\left(x\right)$ dengan $f_1\left(x\right)=5\sec x,\ f_2\left(x\right)=-3\csc x,\ f_3\left(x\right)=2x$

Diperoleh

$f_1'\left(x\right)=5\sec x\tan x$

$f_2'\left(x\right)=-3\left(-\csc x\cot x\right)=3\csc x\cot x$

$f_3'\left(x\right)=2.1x^{1-1}=2x^0=2$

Dengan demikian

$f'\left(x\right)=5\sec x\tan x+3\csc x\cot x+2$

Pembahasan:

Diketahui:

Fungsi $h(x)=\csc^5(2x-3)+4x^2+7$

Ditanya:

$\frac{d}{dx}h(x)$ ?

Jawab:

Secara umum turunan pertama untuk beberapa fungsi sebagai berikut:

Untuk fungsi $y=a\csc^n\left(f\left(x\right)\right)$ turunannya adalah $y'=an\csc^{n-1}\left(f\left(x\right)\right)(-\csc\left(f\left(x\right)\right)\cot(f(x)))f'\left(x\right)$

Untuk fungsi $y=x^n$ turunannya adalah $y'=nx^{n-1}$

Untuk fungsi $y=a$ dengan $a$ suatu konstanta turunannya adalah $y'=0$

Untuk fungsi $y=f\left(x\right)+g\left(x\right)$ turunannya adalah $y'=f'\left(x\right)+g'\left(x\right)$

Fungsi yang diketahui pada soal berbentuk $h\left(x\right)=h_1\left(x\right)+h_2\left(x\right)+h_3(x)$ dengan $h_1(x)=\csc^5(2x-3), h_2(x)=4x^2, h_3(x)=7$

Dimisalkan $f(x)=2x-3$ maka $f'(x)=2$