1.
Pada △ PQR siku-siku di P, berlaku ....
Pembahasan:
Gambarlah △ PQR dengan siku-siku di P. Ingatlah kalau sisi yang berseberangan dengan sudut diberi notasi huruf yang sama, tetapi huruf kecil. Misalnya sisi p berseberangan dengan titik P, dan seterusnya.
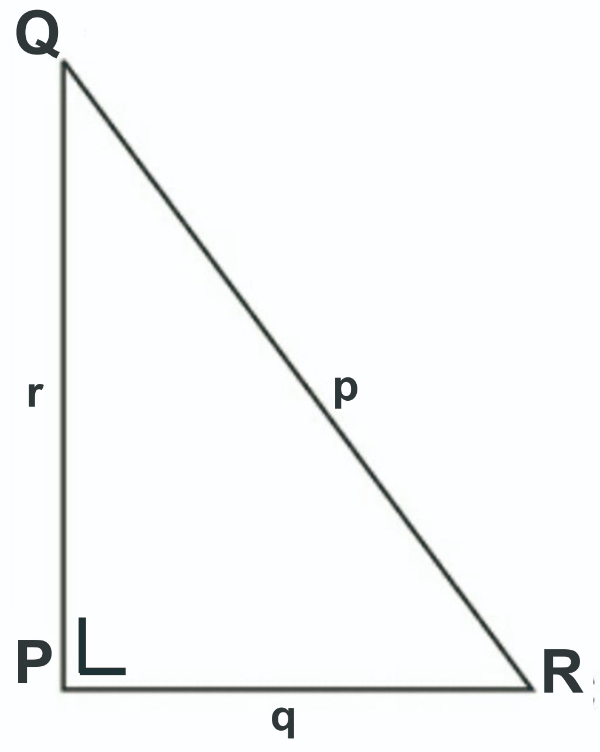
p merupakan garis terpanjang karena berseberangan dengan siku-siku P. Sesuai Teorema Pythagoras, yang benar adalah p2 = q2 + r2.
2.
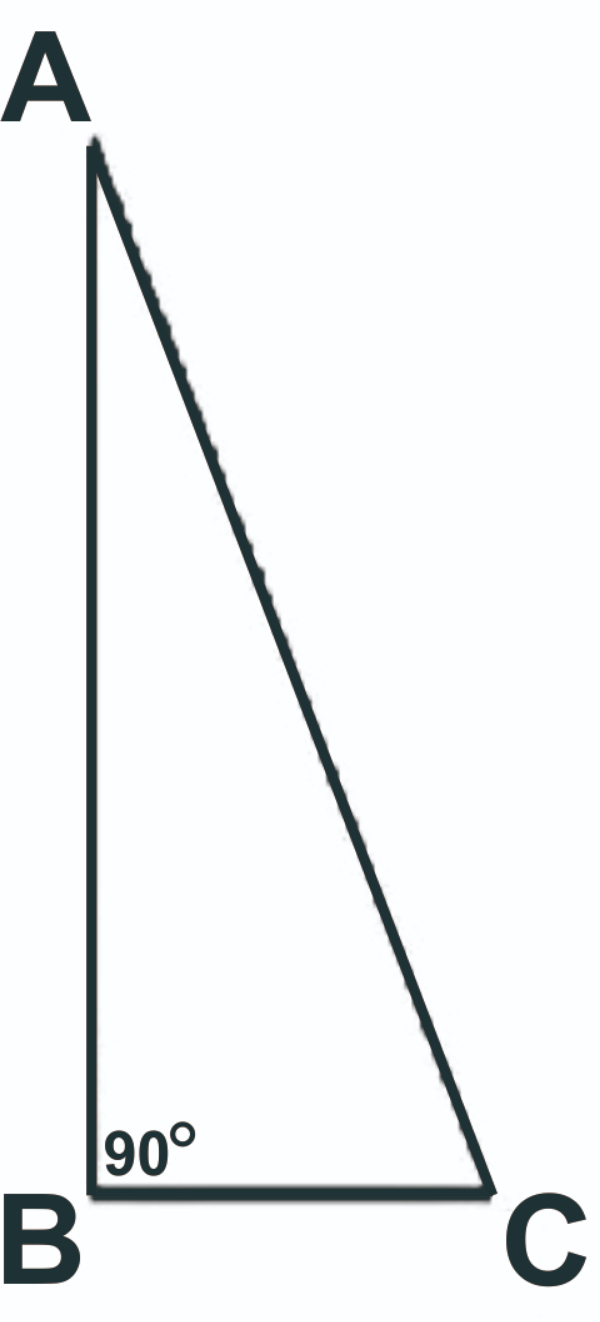
Jika diketahui BC = 7 cm, AB = 24 cm. Tentukan panjang AC!
Pembahasan:
Cara 1
Menggunakan tripel Pythagoras 7, 24, 25 (jika hafal)
Cara 2
Gunakan rumus Pythagoras untuk mencari hipotenusa AC pada △ABC dengan alas BC = 7 cm dan tinggi AB = 24 cm.
AC2 = AB2 + BC2
AC2 = 72 + 242
AC2 =49 + 576 = 625
AC = √625 = 25 cm
3.
Pada △XYZ dengan siku-siku di Z, diketahui panjang XZ = 7 cm dan YZ = 24 cm. Berapakah panjang XY?
Pembahasan:
Cara 1
Menggunakan tripel Pythagoras = 7, 24, 25 (jika ingat)
Cara 2
Menggunakan teorema Pythagoras untuk mencari hipotenusa (sisi miring atau terpanjang) XY pada △XYZ dengan alas XZ = 7 cm dan tinggi YZ = 24 cm.
XY2 = XZ2 + YZ2
XY2= 72 + 242
XY2= 49 + 576 = 625
XY = √625 = 25 cm
4.
Pada △FGH siku-siku di H, diketahui panjang FH = 6 cm dan GH = 7 cm. Berapakah panjang FG?
Pembahasan:
Gunakan rumus Pythagoras untuk mencari hipotenusa FG pada △FGH dengan alas FH = 6 cm dan tinggi GH = 7 cm.
FG2 = FH2 + GH2
FG2= 62 + 72
FG2= 36 + 49 = 85
FG =85 cm
5.
Perhatikan gambar berikut!
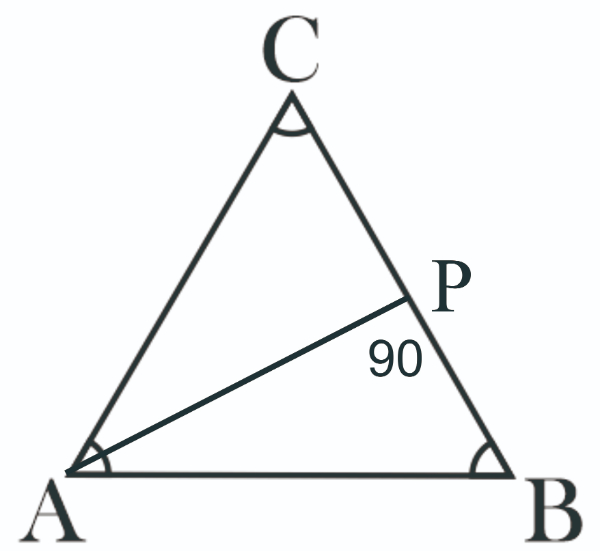
Segitiga ABC adalah segitiga sama sisi. Jika AB = 4 m, maka berapakah panjang AP?
Pembahasan:
Perhatikan bahwa AP merupakan tinggi dari △ABP dengan hipotenusa AB = 4 m dan alas BP yang dihitung sebagai berikut. Karena △ABC adalah segitiga sama sisi, maka BP = BC ÷ 2 = 4 ÷ 2 = 2 m. Gunakan rumus Pythagoras untuk menghitung tinggi AP dari △ABP.
AB2 = AP2 + BP2
AP2 = AB2 - BP2
AP = 16 −4 = 12 m
AP = 23 m
6.
 Jika AC = 10 5 cm dan BC = 10 2 cm, berapakah luas kartu pos tersebut?
Jika AC = 10 5 cm dan BC = 10 2 cm, berapakah luas kartu pos tersebut?
Pembahasan:
Untuk mencari luas kartu pos yang berbentuk persegi panjang, perlu diketahui panjang BC dan lebar AB. Panjang BC diketahui tetapi AB tidak. Jadi harus menghitung AB terlebih dahulu.
Menghitung lebar AB
AB merupakan tinggi dari △ABC dengan hipotenusa AC = 105 cm dan alas BC = 102 cm. Hitung AB dengan rumus Pythagoras seperti berikut ini.
AB2 = AC2 - BC2
AB2 = 500 - 200 = 300
AB = 300= 10 3 cm
Menghitung luas kartu pos
= luas persegi panjang
= panjang × lebar
= BC × AB
= (102)(103) =(100 6) cm2
7.
Kain terpal milik ayah berbentuk persegi panjang dengan ukuran panjang 4 meter dan lebar 2 meter. Berapakah diagonal kain terpal ayah?
Pembahasan:
Diagonal persegi panjang = hipotenusa pada segitiga siku-siku dengan:
- Alas segitiga = panjang persegi panjang = 4 meter
- Tinggi segitiga = lebar persegi panjang = 2 meter
Gunakan rumus Pythagoras untuk menghitung hipotenusa.
(hipotenusa)2 = (alas)2 + (tinggi)2
(hipotenusa)2 = (4)2 + (2)2
(hipotenusa)2 = 16 + 4 = 20
hipotenusa = 20 = 25 meter
Jadi diagonal kain terpal = 25 meter.
8.
Einstein membeli tanah berbentuk segitiga siku-siku seluas 42 m2. Jika salah satu sisi penyiku tanah tersebut 12 m, Berapakah keliling tanah yang dibeli oleh Einstein?
Pembahasan:
Untuk menghitung keliling tanah, perlu diketahui panjang semua sisi segitiga. Salah satu sisi penyiku diketahui, jadi sisi penyiku lainnya dan hipotenusa segitiga masih perlu dicari.
Mencari sisi penyiku lainnya
Sisi penyiku adalah sisi yang membentuk sudut siku-siku, yaitu alas atau tinggi segitiga siku-siku. Katakanlah sisi penyiku yang diketahui adalah alasnya (hasilnya sama jika yang diketahui tingginya). Maka tinggi segitiga dapat dihitung dengan rumus luas segitiga dengan luas = 42 m2 dan alas = 12 m.
Luas segitiga = 2alas×tinggi
42 m2 = 212×tinggi
42 m2 = 6 × tinggi
tinggi = 42 ÷ 6 = 7 m
Jadi tinggi AB = 7 m
Mencari hipotenusa
(hipotenusa)2 = (alas)2 + (tinggi)2
(hipotenusa)2 = 122 + 72
(hipotenusa)2 = 144 + 49 = 193
hipotenusa = √193 m
Mencari keliling segitiga
= alas + tinggi + hipotenusa
= 12 m + 7 m + √193 m
= (19 +√193) m
9.
Vincent memotong kertas origami berbentuk persegi sehingga menjadi 2 segitiga sama besar. Jika diagonal bidang persegi sepanjang 62 cm, maka berapakah panjang sisi origami tersebut?
Pembahasan:
Perhatikan kalau diagonal bidang persegi = hipotenusa segitiga siku-siku dengan sisi penyiku = sisi persegi. Gunakan rumus Pythagoras untuk menghitung panjang sisi persegi.
(diagonal)2 = (sisi)2 + (sisi)2
(62 )2 = 2 (sisi)2
72 = 2 (sisi)2
36 = (sisi)2
sisi = 36 cm = 6 cm
10.
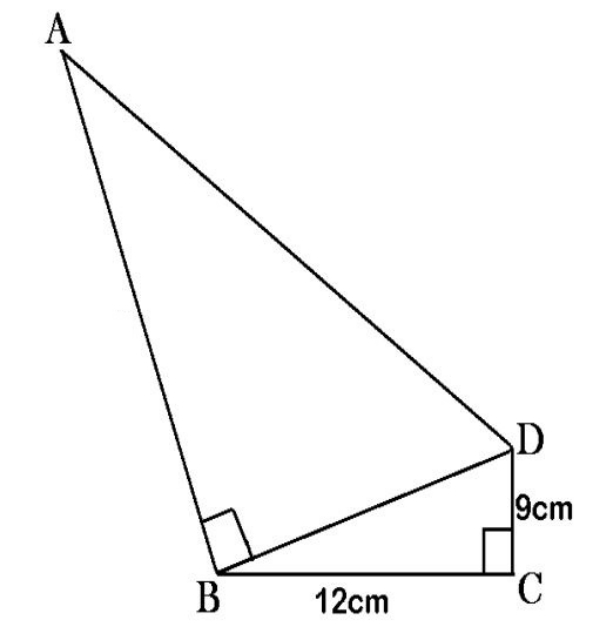
Diketahui BC = 12 cm, CD = 9 cm dan luas △ABD = 150 cm2. Tentukan panjang AB!
Pembahasan:
AB merupakan tinggi dari segitiga siku-siku △ABD, yang dapat dihitung dengan menggunakan rumus luas segitiga jika luas △ABD dan alas BD diketahui. Luas △ABD sudah diketahui, jadi tinggal mencari BD.
Mencari BD
Perhatikan bahwa BD merupakan hipotenusa dari △BCD, yang mempunyai alas BC = 12 cm dan tinggi CD = 9 cm. Gunakan rumus Pythagoras untuk menemukan hipotenusa BD.
BD2 = BC2+CD2
BD2 = 122+92
BD2 = 144 + 81
BD2 = 225
BD = 15 cm
atau juga bisa menggunakan tripel Pythagoras 9, 12, 15 (jika ingat).
Mencari AB
Gunakan rumus luas segitiga untuk menghitung tinggi AB jika diketahui luas △ABD = 150 cm2 dan alas BD = 15 cm.
L△ABD = 2alas×tinggi
150 = 215×AB
AB = 15150×2 = 20 cm
