Pembahasan:
Diketahui:
Jaring-jaring prisma seperti gambar berikut.
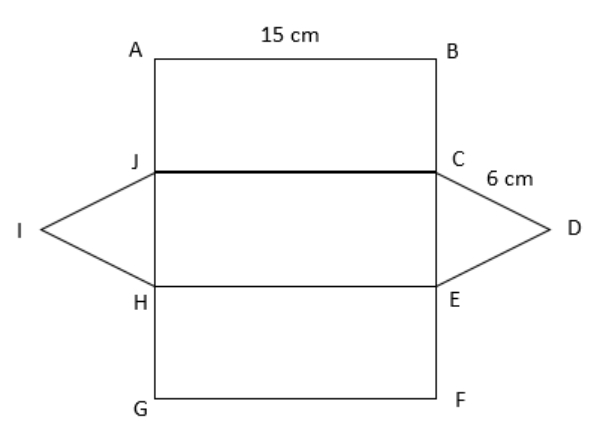
Alas prisma (△CDE) segitiga sama sisi.
Ditanya:
Luas permukaan prisma tersebut?
Jawab:
Karena alas prima (△CDE) berupa segitiga sama sisi, maka panjang BC = CE = EF = 6 cm. Oleh karena itu, persegi panjang ABCJ, JCEH, dan EFGH memiliki ukuran yang sama yaitu
panjang p = 15 cm dan
lebar l = 6 cm.
Rumus luas persegi panjang adalah
L=p×l
sehingga luas persegi panjang ABCJ adalah
L1=15×6=90 .
Jadi luas persegi panjang ABCJ adalah 90 cm2
Selanjutnya, perhatikan △CDE berikut!
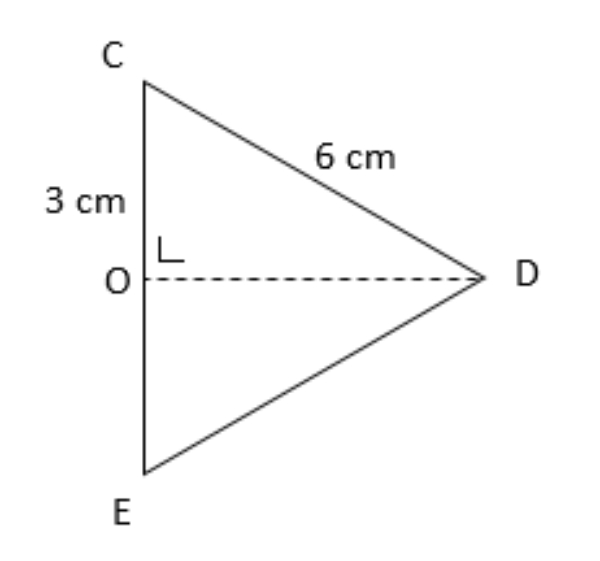
Titik O merupakan titik tengah garis CE. Diperhatikan △CDO!
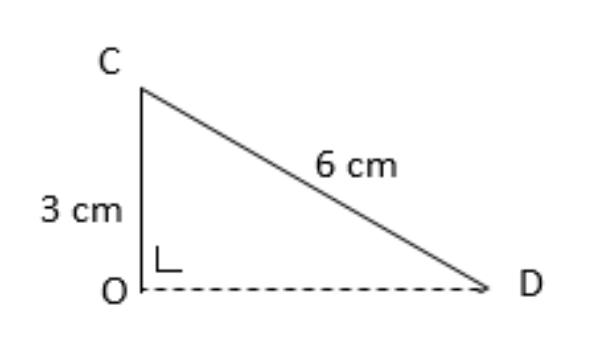
Berdasarkan Teorema Pythagoras diperoleh
CD2=OC2+OD2
OD2=CD2−OC2
OD=CD2−OC2
OD=62−32
OD=36−9
OD=27
OD=9×3
OD=33
Artinya △CDE memiliki
alas a = 6 cm dan
tinggi t = 33 cm.
Rumus luas segitiga adalah
L=2a×t
sehingga diperoleh luas △CDE adalah
L2=26×33=93
Jadi luas △BCO adalah 93 cm2.
Pada jaring-jaring prisma tersebut terdapat 3 persegi panjang yang memiliki ukuran yang sama dengan persegi panjang ABCJ dan 2 segitiga yang memiliki ukuran yang sama dengan △CDE.
Akibatnya luas permukaan prisma tersebut adalah
L=3.L1+2.L2
L=3.90+2.93
L=270+183
Jadi luas permukaan prisma tersebut adalah 270+183 cm2
