Pembahasan:
Diketahui:
Sebuah dadu dan sebuah uang logam dilempar secara bersama-sama sebanyak 24 kali.
Ditanya:
Frekuensi harapan muncul angka dan mata dadu bilangan genap?
Dijawab:
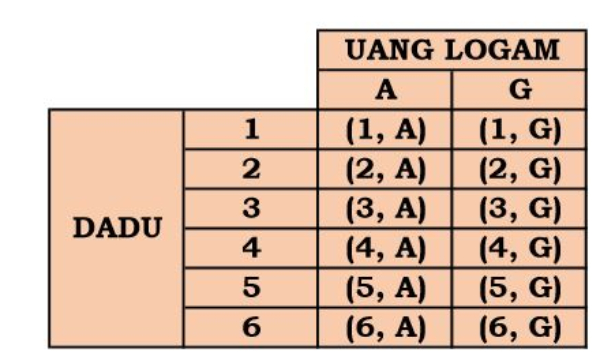
A merupakan lambang angka dan G merupakan lambang gambar.
Banyaknya titik sampel S adalah
n(S) = 12.
Kejadian B muncul angka adalah
B = {(1, A), (2, A), (3, A), (4, A), (5, A), (6, A)}.
Kejadian D muncul mata dadu bilangan genap adalah
D = {(2, A), (2, G), (4, A), (4, G), (6, A), (6, G)}.
Kejadian B ∩ D muncul angka dan mata dadu bilangan genap adalah
B ∩ D = {(2, A), (4, A), (6, A)}.
Banyaknya kejadian B ∩ D adalah
n(B ∩ D) = 3.
Peluang kejadian B ∩ D adalah
P(B ∩ D)
= n(S)n(B ∩ D)
= 123
= 41.
Frekuensi harapan kejadian B ∩ D adalah
Fh(B ∩ D)
= P(B ∩ D) × Banyak percobaan
= 41 × 24
= 6.
Jadi, frekuensi harapan muncul angka dan mata dadu bilangan genap adalah 6 kali.
